
分析 假设a≥$\frac{1}{3}$,b≥$\frac{1}{3}$,c≥$\frac{1}{3}$,则a+b+c≥1,从而与a+b+c<1矛盾,即可证明结论.
解答 证明:假设a≥$\frac{1}{3}$,b≥$\frac{1}{3}$,c≥$\frac{1}{3}$,则a+b+c≥1,
与a+b+c<1矛盾,
所以a,b,c中至少有一个小于$\frac{1}{3}$.
点评 反证法是一种简明实用的数学证题方法,也是一种重要的数学思想.相对于直接证明来讲,反证法是一种间接证法.它是数学学习中一种很重要的证题方法.其实质是运用“正难则反”的策略,从否定结论出发,通过逻辑推理,导出矛盾.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
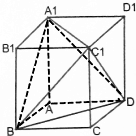
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com