
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() 且过点
且过点![]() 椭圆C与
椭圆C与![]() 轴的交点为A、B(点A位于点B的上方),直线
轴的交点为A、B(点A位于点B的上方),直线![]() 与椭圆C交于不同的两点M、N(点M位于点N的上方).
与椭圆C交于不同的两点M、N(点M位于点N的上方).

(1)求椭圆C的方程;
(2)求△OMN面积的最大值;
(3)求证:直线AN和直线BM交点的纵坐标为常值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,证明见解析
,证明见解析
【解析】
(1)由题可知![]() ,椭圆过点
,椭圆过点![]() 所以将点代入可得
所以将点代入可得![]() ,再结合椭圆的关系式即可求解
,再结合椭圆的关系式即可求解
(2)联立椭圆和直线的方程,表示出韦达定理,再表示出弦长公式,用点到直线距离公式表示出点![]() 到直线距离,进一步化简求值即可
到直线距离,进一步化简求值即可
(3)结合(2)中的韦达定理,表示出直线![]() 与直线
与直线![]() 方程,再联立求解即可
方程,再联立求解即可
(1)由题可知![]() ,又椭圆过点
,又椭圆过点![]() 所以将点
所以将点![]() 代入椭圆的标准方程可得
代入椭圆的标准方程可得![]() ,结合椭圆的关系式
,结合椭圆的关系式![]() ,可得
,可得![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]()
(2)设![]() ,联立方程组
,联立方程组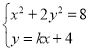 ,
,
化简得![]() ,由△
,由△![]() ,
,
解得![]() ,由韦达定理,得
,由韦达定理,得![]() ,
,![]() ,
,
![]() ,点
,点![]() 到直线距离
到直线距离![]() ,则
,则![]()
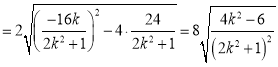 ,令
,令![]() ,
,![]() ,则
,则
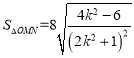 可代换为
可代换为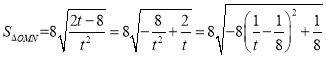
当![]() 时,
时,![]() 取到最大值,
取到最大值,![]()
(3)借用(2)中的韦达定理,直线![]() 的方程
的方程![]() ①
①
直线![]() 的方程
的方程![]() ②,联立①②,
②,联立①②,
得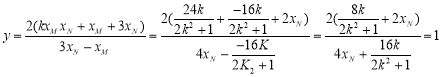
即![]()
![]() 直线
直线![]() 与直线
与直线![]() 的交点
的交点![]() 在定直线
在定直线![]() 上.
上.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若正项数列![]() 满足:
满足:![]() ,则称此数列为“比差等数列”.
,则称此数列为“比差等数列”.
(1)试写出一个“比差等数列”的前![]() 项;
项;
(2)设数列![]() 是一个“比差等数列”,问
是一个“比差等数列”,问![]() 是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
是否存在最小值,如存在,求出最小值;如不存在,请说明理由;
(3)已知数列![]() 是一个“比差等数列”,
是一个“比差等数列”,![]() 为其前
为其前![]() 项的和,试证明:
项的和,试证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(2)当![]() 时,判断函数
时,判断函数![]() 的单调性,并证明;
的单调性,并证明;
(3)求实教![]() 的范围,使得对于区间
的范围,使得对于区间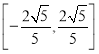 上的任意三个实数
上的任意三个实数![]() ,都存在以
,都存在以![]() 为边长的三角形.
为边长的三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为![]() ,第七个音的频率为
,第七个音的频率为![]() ,则
,则![]() =
=
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 及点
及点![]() ,若直线
,若直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,且
,且![]() (
( ![]() 为坐标原点),椭圆
为坐标原点),椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若斜率为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 以
以![]() 、
、![]() 为焦点,且过点
为焦点,且过点![]()
(1)求双曲线![]() 与其渐近线的方程;
与其渐近线的方程;
(2)是否存在斜率为2的直线![]() 与双曲线
与双曲线![]() 右支相交于
右支相交于![]() 两点,且
两点,且![]() (
(![]() 为坐标原点).若存在,求直线
为坐标原点).若存在,求直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】作为交通重要参与者的行人,闯红灯通行频有发生,带来了较大的交通安全隐患.在某十字路口,交警部门从穿越该路口的行人中随机抽取了200人进行调查,得到不完整的![]() 列联表如图所示:
列联表如图所示:
年龄低于30岁 | 年龄不低于30岁 | 合计 | |
闯红灯 | 60 | 80 | |
未闯红灯 | 80 | ||
合计 | 200 |
(1)将![]() 列联表补充完整;
列联表补充完整;
(2)是否有99.9%的把握认为行人是否闯红灯与年龄有关.
参考公式及数据: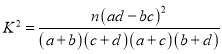 ,其中
,其中![]() .
.
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com