数学英语物理化学 生物地理
数学英语已回答习题未回答习题题目汇总试卷汇总练习册解析答案
分析：利用函数的单调性是讨论函数值域的重要方法.直接求导计算繁杂.通过换元t=,将问题转化为求函数y=t4-4t2+4t+4在［0，+∞］上的值域.
解：设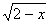≥0,则x=2-t2.y=t4-4t2+4t+4(t≥0),设f(t)=t4-4t2+4t+4,f′(t)=4t3-8t+4
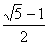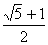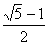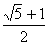=4(t-1)(t-)(t+).令f′（t）=0得t1=1,t2=,t3=- (舍去).
当 0≤t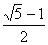＜,f′(t)＞0,当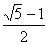＜t＜1时，f′(t)＜0,当t＞1时，f′(t)＞0.又f(0)=4,f(1)=5，f(t)=+∞.故函数y=f(t)的最小值为4无最大值.即所求函数的值域是［4，+∞).
科目：高中数学 来源： 题型：
国际学校优选 - 练习册列表 - 试题列表
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
的值域.
阅读快车系列答案
≥0,则x=2-t2.y=t4-4t2+4t+4(t≥0),设f(t)=t4-4t2+4t+4,f′(t)=4t3-8t+4
)(t+
).令f′（t）=0得t1=1,t2=
,t3=-
(舍去).
,f′(t)＞0,当
＜t＜1时，f′(t)＜0,当t＞1时，f′(t)＞0.又f(0)=4,f(1)=5，
f(t)=+∞.故函数y=f(t)的最小值为4无最大值.即所求函数的值域是［4，+∞).
