
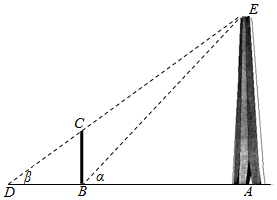
 某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.
某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.分析 (I)根据三角函数的定义用H,h,tanα,tanβ表示出AD,BD,AB,根据AD-AB=DB列方程解出H.
(II)根据两角差的正切公式得出tan(α-β)关于H,h,d的函数关系式,使用基本不等式求出tan(α-β)取得最大值的条件.
解答 解:(I)∵tanβ=$\frac{H}{AD}$=$\frac{h}{BD}$,tanα=$\frac{H}{AB}$,
∴AD=$\frac{H}{tanβ}$,BD=$\frac{h}{tanβ}$,AB=$\frac{H}{tanα}$.
∵AD-AB=DB,∴$\frac{H}{tanβ}-\frac{H}{tanα}=\frac{h}{tanβ}$,
解得:$H=\frac{htanα}{tanα-tanβ}=\frac{2×1.21}{1.21-1.17}=60.5(m)$.
∴胜利塔的高度H是60.5m.
(II)∵tanα=$\frac{H}{d}$,tanβ=$\frac{H}{AD}=\frac{h}{BD}=\frac{H-h}{d}$,
∴tan(α-β)=$\frac{tanα-tanβ}{1+tanα•tanβ}$=$\frac{\frac{H}{d}-\frac{H-h}{d}}{1+\frac{H}{d}•\frac{H-h}{d}}$=$\frac{hd}{{d}^{2}+H(H-h)}=\frac{h}{d+\frac{H(H-h)}{d}}$.
∵d+$\frac{H(H-h)}{d}$≥2$\sqrt{H(H-h)}$,
(当且仅当d=$\sqrt{H(H-h)}$=$\sqrt{60×58}$=2$\sqrt{870}$时取等号)
∵0<β<α<$\frac{π}{2}$,则0<α-β<$\frac{π}{2}$,
∴故当$d=2\sqrt{870}$时,tan(α-β)最大.
点评 本题考查了解三角形的实际应用,三角函数的定义,基本不等式的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
| AQI指数M | 900 | 700 | 300 | 100 |
| 空气可见度y(千米) | 0.5 | 3.5 | 6.5 | 9.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直线x=-1对称 | B. | 直线x=1对称 | C. | 原点对称 | D. | y轴对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com