
分析 (1)方法一:由f(x)是开口向上的抛物线,可得:M=max{f(0),f(2)},即$\left\{\begin{array}{l}f(0)=-a-b≤1\\ f(2)=3a+b≤1\end{array}\right.$,两式相加可得a的最大值;
方法二:$a=\frac{f(2)-2f(1)+f(0)}{2}$=$\frac{f(2)+f(0)}{2}$,结合M≤1,可得a的最大值
(2)存在${f_{min}}(x)+f({x_2})>\frac{3}{2}a$,使${f_{min}}(x)+f({x_2})>\frac{3}{2}a$,结合二次函数的图象和性质,分类讨论,最后综合讨论结果,可得答案.
解答 解:(1)∵f(x)过点(1,0),
∴f(1)=a+b+c=0,…(1分)
∴c=-a-b,f(x)=ax2+bx-a-b
∵f(x)是开口向上的抛物线,
∴M=max{f(0),f(2)}…(3分)
∴$M≤1?\left\{\begin{array}{l}f(0)=-a-b≤1\\ f(2)=3a+b≤1\end{array}\right.$…(5分)
两式相加得a≤1,即a的最大值为1…(6分)
解法二:由$\left\{{\begin{array}{l}{f(1)=a+b+c}\\{f(2)=4a+2b+c}\\{f(0)=c}\end{array}}\right.$
解得:$a=\frac{f(2)-2f(1)+f(0)}{2}$=$\frac{f(2)+f(0)}{2}$≤$\frac{1+1}{2}$=1 …(6分)
(2)由题意,存在${f_{min}}(x)+f({x_2})>\frac{3}{2}a$,使${f_{min}}(x)+f({x_2})>\frac{3}{2}a$,
∴${f_{min}}(x)+{f_{max}}(x)>\frac{3}{2}a$…(8分)
∵a+b+c=0
∴f(x)=ax2+bx-a-b其对称轴为$x=-\frac{b}{2a}$
①当$-\frac{b}{2a}<0$,即$\frac{b}{a}>0$时,f(x)在[0,2]上单调递增,
∴${f_{min}}(x)+{f_{max}}(x)=f(0)+f(2)=-a-b+3a+b=2a>\frac{3}{2}a$
∴$\frac{b}{a}$>0均符合题意 …(10分)
②当$0≤-\frac{b}{2a}<1$,即$-2<\frac{b}{a}≤0$时,
f(x)在[0,$-\frac{b}{2a}$]上递减,在[$-\frac{b}{2a}$,2]上递增且f(0)<f(2),
∴${f}_{min}(x)+{f}_{max}(x)=f(-\frac{b}{2a})+f(2)=-\frac{{b}^{2}}{4a}-a-b+3a+b=-\frac{{b}^{2}}{4a}+2a$
∴由$-\frac{b^2}{4a}+2a>\frac{3}{2}a$得:$-\sqrt{2}<\frac{b}{a}≤0$,符合题意 …(12分)
③当$1≤-\frac{b}{2a}<2$,即$-4<\frac{b}{a}≤-2$时,
f(x)在[0,$-\frac{b}{2a}$]上递减,在[$-\frac{b}{2a}$,2]上递增且f(0)≥f(2),
${f}_{min}(x)+{f}_{max}(x)=f(-\frac{b}{2a})+f(0)=-\frac{{b}^{2}}{4a}-a-b-a-b=-\frac{{b}^{2}}{4a}-2a-2b$
∴由$-\frac{b^2}{4a}-2a-2b>\frac{3}{2}a$得:$-4-\sqrt{2}<\frac{b}{a}<-4+\sqrt{2}$
∴$-4<\frac{b}{a}<-4+\sqrt{2}$符合题意 …(13分)
④当$-\frac{b}{2a}≥2$即$\frac{b}{a}≤-4$时,f(x)在[0,2]上单调递减,
∴${f_{min}}(x)+{f_{max}}(x)=f(2)+f(0)=3a+b-a-b=2a>\frac{3}{2}a$,
∴$\frac{b}{a}≤-4$均符合题意 …(14分)
综上所述:∴$\frac{b}{a}<-4+\sqrt{2}$或$\frac{b}{a}>-\sqrt{2}$…(15分)
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:解答题
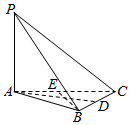 在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D,E分别为BC,CA的中点.
在三棱锥P-ABC中,PA⊥平面ABC,△ABC为正三角形,D,E分别为BC,CA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
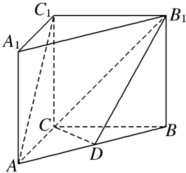 (用空间向量坐标表示解答)如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.
(用空间向量坐标表示解答)如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1=2,AC⊥BC,D为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 城市 | A | B | C | D | E |
| 4S店个数x | 3 | 4 | 6 | 5 | 2 |
| 销量y(台) | 28 | 30 | 35 | 31 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
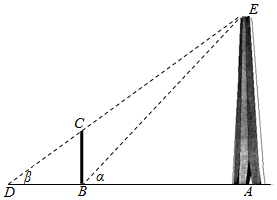 某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.
某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
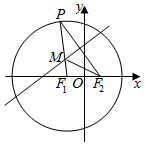 如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com