
| 城市 | A | B | C | D | E |
| 4S店个数x | 3 | 4 | 6 | 5 | 2 |
| 销量y(台) | 28 | 30 | 35 | 31 | 26 |
分析 (I)根据回归系数公式计算回归系数,得出回归方程;
(II)X的取值为0,1,2,3,分别计算各取值的概率,得出X的分布列和数学期望.
解答 解:(Ⅰ)$\overline x=4,\overline y=30$,∴$\hat b=\frac{(3-4)(28-30)+(4-4)(30-30)+(6-4)(35-30)+(5-4)(31-30)+(2-4)(26-30)}{{{{(3-4)}^2}+{{(4-4)}^2}+{{(6-4)}^2}+{{(5-4)}^2}+{{(2-4)}^2}}}=2.1$,$\hat a=30-2.1×4=21.6$,
∴y关于x的线性回归方程为:$\hat y=2.1x+21.6$.
(Ⅱ)X的可能取值为:0,1,2,3.
$P(X=0)=\frac{C_6^4}{C_9^4}=\frac{5}{42}$,$P(X=1)=\frac{C_3^1C_6^3}{C_9^4}=\frac{10}{21}$,$P(X=2)=\frac{C_3^2C_6^2}{C_9^4}=\frac{5}{14}$,$P(X=3)=\frac{C_3^3C_6^1}{C_9^4}=\frac{1}{21}$.
X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{5}{42}$ | $\frac{10}{21}$ | $\frac{5}{14}$ | $\frac{1}{21}$ |
点评 本题考查了线性回归方程的求解,离散型随机变量的分布列和数学期望,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | m | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
| AQI指数M | 900 | 700 | 300 | 100 |
| 空气可见度y(千米) | 0.5 | 3.5 | 6.5 | 9.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
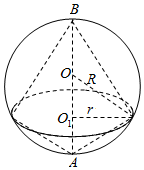 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com