
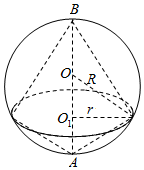
 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$. 分析 利用球的半径,求出球的面积,然后求出圆锥的底面积,求出两个圆锥体积的和及球的体积,可得答案.
解答 解:球的半径为:R;
则球的表面积为:4πR2,圆锥的底面积为:$\frac{3}{16}$×4πR2=$\frac{3}{4}$πR2,
两个圆锥的体积和为:$\frac{1}{3}$×($\frac{3}{4}$πR2)×(BO1+O1A)=$\frac{1}{3}$×($\frac{3}{4}$πR2)×2R=$\frac{1}{2}$πR3,
球的体积为:$\frac{4}{3}$•π•r3,
故两个圆锥的体积之和与球的体积之比为:$\frac{\frac{1}{2}π{R}^{3}}{\frac{4}{3}π{R}^{3}}$=$\frac{3}{8}$.
故答案为:$\frac{3}{8}$.
点评 本题考查的知识点是球的体积和表面积,其中熟练掌握球和圆锥的体积公式,是解答的关键.


科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 12$\sqrt{3}$ | C. | 18$\sqrt{3}$ | D. | 36$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 城市 | A | B | C | D | E |
| 4S店个数x | 3 | 4 | 6 | 5 | 2 |
| 销量y(台) | 28 | 30 | 35 | 31 | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -3 | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com