
分析 方法一,利用列举法,即可出答案,
方法二,利用排列组合的知识即可求出.
解答 解法一:把每枚圆珠笔上号码,一等品分别记作A,B,C,D,二等品分别记作E,F.
依次不放回从盒子中取出2枚圆珠笔,得到的两个标记分别为x 和y,则(x,y) 表示一次抽取的结果,即基本事件.
由于是随机抽取,所以抽取到任何事件的概率相等.
用M 表示“抽到的2枚圆珠笔中有二等品”,
M1 表示“仅第一次抽取的是二等品”,
M2 表示“仅第二次抽取的是二等品”,
M3 表示“两次抽取的都是二等品”.
M1 和M2 中的基本事件个数都为8,
M3 中的基本事件为2,
全部基本事件的总数为30.
(1)由于M1 和M2 是互斥事件,记N=M1∪M2,
∴恰有一枚一等品的概率$P(N)=P({A_1})+P({A_2})=\frac{8}{30}+\frac{8}{30}=\frac{8}{15}$.
(2)由于M1,M2 和M3 是互斥事件,且M=M1∪M2∪M3,
∴$P(M)=P({M_1})+P({M_2})+P({M_3})=\frac{8}{30}+\frac{8}{30}+\frac{2}{30}=\frac{3}{5}$.
解法二:(1)恰有一枚一等品的概率${P_1}=\frac{C_4^1C_2^1}{C_6^2}=\frac{8}{15}$.
(2)有二等品的概率${P_2}=\frac{C_4^1C_2^1+C_2^2}{C_6^2}=\frac{3}{5}$,
或${P_2}=1-\frac{C_4^2}{C_6^2}=1-\frac{2}{5}=\frac{3}{5}$.
点评 本题考查概率的计算,解题时要认真审题,注意排列组合知识的合理运用,是基础题.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
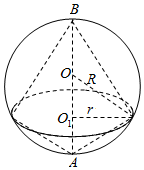 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 34 | 38 | 64 |
| A. | 68 | B. | 67 | C. | 66 | D. | 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25 | B. | 35 | C. | 840 | D. | 820 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com