
分析 (1)求出f(x)的导数,可得切线的斜率,由两直线垂直的条件:斜率之积为-1,解方程可得a;
(2)求得f(x)的导数,讨论a≥0时,a<0时,由导数大于0,可得增区间;导数小于0,可得减区间;
(3)讨论a>0,a=0,a<0,运用函数的单调性和函数的零点存在定理,以及函数的最小值大于0,解不等式即可得到所求范围.
解答 解:(1)f(x)=x+alnx的导数为$f'(x)=\frac{x+a}{x}(x>0)$.
由题意在x=2处的切线与直线x-y+1=0垂直,
可得$f'(2)=\frac{2+a}{2}=-1$,解得a=-4;
(2)因$f'(x)=\frac{x+a}{x}(x>0)$,
当a≥0时,在x∈(0,+∞)时,f'(x)>0,可得f(x)的单调区间是(0,+∞);
当a<0时,f(x)与f'(x)在定义域上的情况如下:
| x | (0,-a) | -a | (-a,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,考查分类讨论的思想方法,同时考查函数的零点问题的解法,注意运用函数的零点存在定理,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
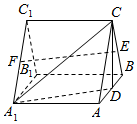 如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等,D,E,F分别为棱AB,BC,A1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,-$\frac{1}{2}$] | B. | [-1,0] | C. | [0,1] | D. | [1,$\frac{3}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| AQI指数 | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
| 频数 | 3 | 6 | 12 | 6 | 3 |
| AQI指数M | 900 | 700 | 300 | 100 |
| 空气可见度y(千米) | 0.5 | 3.5 | 6.5 | 9.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.
已知正棱锥P-ABCD中,PA⊥平面ABCD,△PAC为等腰直角三角形,PA=6,底面ABCD为平行四边形,且∠ABC+∠ADC=90°,E为线段AD的中点,F在线段PD上运动,记$\frac{PF}{PD}$=λ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
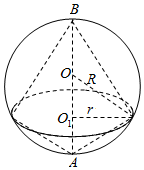 一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.
一个透明的球形装饰品内放置了两个公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,圆锥圆锥底面面积是这个球面面积的$\frac{3}{16}$,设球的半径为R,圆锥底面半径为r.则两个圆锥的体积之和与球的体积之比为$\frac{3}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温x(℃) | 18 | 13 | 10 | -1 |
| 用电量y(度) | 24 | 34 | 38 | 64 |
| A. | 68 | B. | 67 | C. | 66 | D. | 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com