
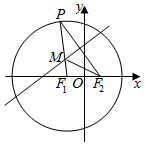
 如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.分析 (1)根据题意,|MP|=|MF2|,则|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|,故M的轨迹C是以F1,F2为焦点,长轴长为4的椭圆,从而可求动点M的轨迹C的方程.
(2)设直线l的方程为x=my+1,设A(x1,y1),B(x2,y2),与椭圆方程联立化为(3m2+4)y2+6my-9=0,再利用弦长公式与点到直线的距离公式即可得出.
解答 解:(1)根据题意,|MP|=|MF2|,
则|MF1|+|MF2|=|MF1|+|MP|=4>|F1F2|,
故M的轨迹C是以F1,F2为焦点,长轴长为4的椭圆,a=2,c=1,
所以b=$\sqrt{3}$,
所以点M的轨迹方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)设直线l的方程为x=my+1,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1,
可得3(my+1)2+4y2=12,
∴(3m2+4)y2+6my-9=0,
设A(x1,y1),B(x2,y2),则y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
∴E到直线l的距离为d=$\frac{3}{\sqrt{1+{m}^{2}}}$,|AB|=$\sqrt{1+{m}^{2}}$|y1-y2|
∴△ABE面积S=$\frac{1}{2}•$$\frac{3}{\sqrt{1+{m}^{2}}}•$$\sqrt{1+{m}^{2}}$|y1-y2|=18$\sqrt{\frac{{m}^{2}+1}{(3{m}^{2}+4)^{2}}}$,
设3m2+4=t(t≥4),则S=18$\sqrt{\frac{{m}^{2}+1}{(3{m}^{2}+4)^{2}}}$=18$\sqrt{\frac{t-1}{{3t}^{2}}}$=18$\sqrt{-\frac{1}{3}(\frac{1}{t}-\frac{1}{2})^{2}+\frac{1}{12}}$,
∵t≥4,
∴t=4,m=0时,△ABE面积的最大值为$\frac{9}{2}$.
点评 本题考查椭圆的定义与方程、直线与椭圆相交弦长问题、点到直线的距离公式,考查了推理能力与计算能力,属于属于中档题,确定M的轨迹C是以F1,F2为焦点,长轴长为4的椭圆关键.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
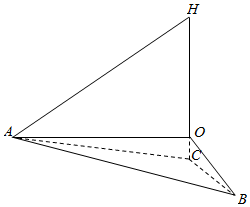 某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点 A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为( )
某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:在C处(点C在水平地面下方,O为CH与水平地面ABO的交点)进行该仪器的垂直弹射,水平地面上两个观察点 A、B两地相距100米,∠BAC=60°,其中A到C的距离比B到C的距离远40米.A地测得该仪器在C处的俯角为∠OAC=15°,A地测得最高点H的仰角为∠HAO=30°,则该仪器的垂直弹射高度CH为( )| A. | $210({\sqrt{6}+\sqrt{2}})$米 | B. | $140\sqrt{6}$米 | C. | $210\sqrt{2}$米 | D. | $210({\sqrt{6}-\sqrt{2}})$米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com