
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 由题意x∈(0,π) 当x∈(0,π) 且x≠$\frac{π}{2}$时,(x-$\frac{π}{2}$)f′(x)>0,以$\frac{π}{2}$为分界点进行讨论,确定函数的单调性,利用函数的图形,画出草图进行求解,即可得到结论
解答 解:∵当x∈[0,π]时,0<f(x)<1,f(x)为偶函数,
∴当x∈[-π,2π]时,0<f(x)<1;
当x∈(0,π) 且x≠$\frac{π}{2}$时,(x-$\frac{π}{2}$)f′(x)>0,
∴x∈[0,$\frac{π}{2}$]时,f(x)为单调减函数;x∈[$\frac{π}{2}$,π]时,f(x)为单调增函数,
∵x∈[0,π]时,0<f(x)<1,
在R上的函数f(x)是最小正周期为2π的偶函数,在同一坐标系中作出y=sinx和y=f(x)草图象如下,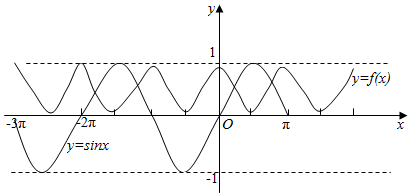
由图知y=f(x)-sinx在[-3π,π]上的零点个数为4个.
故选:B.
点评 本题考查函数的单调性,考查函数的零点,考查函数的周期性与奇偶性,利用数形结合的思想来求解,会化难为易.


科目:高中数学 来源: 题型:解答题
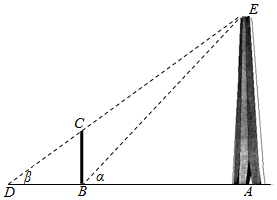 某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.
某兴趣小组测量渡江战役纪念馆前的胜利之塔的高度H(单位:m)如示意图,垂直放置的标杆BC高度h=2m,仰角∠ABE=α,∠ADE=β.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A. | 3.25 | B. | 2.6 | C. | 2.2 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
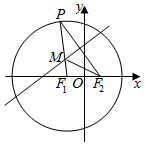 如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.
如图,已知P是以F1(-1,0),以4为半径的圆上的动点,P与F2(1,0)所连线段的垂直平分线与线段PF1交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
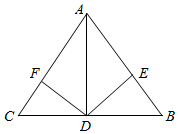 如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC
如图,AD是△ABC边BC上的高,DE⊥AB,DF⊥AC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1只是坏的概率 | B. | 2只都是坏的概率 | ||
| C. | 恰有1只是好的概率 | D. | 至多1只是坏的概率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com