
| A. | 若a≠b,则$\frac{a+b}{2}>\sqrt{ab}$ | B. | 若a>0,b>0,则$\frac{a+b}{2}≥\sqrt{ab}$ | ||
| C. | 若$\frac{a+b}{2}≥\sqrt{ab}$,则a>0,b>0 | D. | 若$\frac{a+b}{2}>\sqrt{ab}$,则a≠b |
分析 根据基本不等式的性质分别进行判断即可.
解答 解:A.当a=-1,b=-3时,不等式$\frac{a+b}{2}>\sqrt{ab}$不成立,故A错误,
B.若a>0,b>0,则$\frac{a+b}{2}≥\sqrt{ab}$,成立,故B正确,
C.若$\frac{a+b}{2}≥\sqrt{ab}$,则ab≥0,a+b≥0,
∵ab≠0,∴ab>0,a+b>0,即a>0,b>0,成立,故C正确,
D.若$\frac{a+b}{2}>\sqrt{ab}$,则a,b>0,
且$\frac{a+b}{2}-\sqrt{ab}=\frac{a-2\sqrt{ab}+b}{2}$>0,即$\frac{(\sqrt{a}-\sqrt{b})}{2}$>0,
则$\sqrt{a}≠\sqrt{b}$,即a≠b,
故D正确,
故选:A
点评 本题主要考查命题的真假判断,涉及基本不等式的性质和应用,注意基本不等式成立的条件.


 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
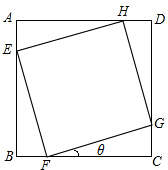 如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).
如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin140°<sin30° | B. | cos140°<cos130° | C. | tan40°<tan30° | D. | sin40°<sin30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com