练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．函数y=log${\;}_{\frac{1}{2}}$（-x2+6x-5）的单调递减区间为（1，3]．

    分析 先求出函数的定义域，然后利用复合函数的单调性确定函数f（x）的单调递减区间．

    解答 解：要使函数有意义，则-x2+6x-5＞0，解得x∈（1，5），
    设t=-x2+6x-5，则函数在（1，3]上单调递增，在[3，5）上单调递减．
    因为函数log${\;}_{\frac{1}{2}}$t在定义域上为减函数，
    所以由复合函数的单调性性质可知，则此函数的单调递减区间是（1，3]．
    故答案为：（1，3]．

    点评 本题主要考查了复合函数的单调性以及单调区间的求法．对应复合函数的单调性，一要注意先确定函数的定义域，二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断，判断的依据是“同增异减”．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．若α∈（0，π），且$cosα+sinα=-\frac{1}{5}$，则tan2α=-$\frac{24}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．曲线C的参数方程为$\left\{{\begin{array}{l}{x=sinα-cosα}\\{y=2sinαcosα}\end{array}}\right.（α为参数）$，则它的普通方程为（　　）
    A．y=x2+1B．y=-x2+1C．$y=-{x^2}+1，x∈[{-\sqrt{2}，\sqrt{2}}]$D．y=x2+1，x∈[-$\sqrt{2}$，$\sqrt{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知函数f（x）=ax3+bx（a≠0）在x=1处取得极大值2，g（x）=$\frac{f（x）}{x}$+3lnx．
    （I）函数f（x）在点（1，2）处的切线方程；
    （Ⅱ）若函数g（x）的图象恒在直线y=x+m的下方，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．2016年04月13日“山东济南非法经营疫苗系列案件”披露后，引发社会高度关注，引起公众、受种者和儿童家长对涉案疫苗安全性和有效性的担忧．为采取后续处置措施提供依据，保障受种者的健康，尽快恢复公众接种疫苗的信心，科学严谨地分析涉案疫苗接种给受种者带来的安全性风险和是否有效，对某疫苗预防疾病的效果，进行动物实验，得到统计数据如表，现从所有试验动物中任取一只，取到“注射疫苗”动物的概率为$\frac{2}{5}$．
    （1）求2×2列联表中的数据x，y，A，B的值；
    未发病发病合计
    未注射疫苗20xA
    注射疫苗30yB
    合计5050100
    （2）绘制发病率的条形统计图，并判断疫苗是否有效？
    （3）能够有多大把握认为疫苗有效？
    附：${{K}^2}=\frac{{n{{（{ad-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
    P（ K2≤K0）0.050.010.0050.001
    K03.8416.6357.87910.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．圆C的极坐标方程为ρ=2$\sqrt{2}$cos（θ+$\frac{π}{4}$），则圆心C的极坐标为（　　）
    A．（$\sqrt{2}$，$\frac{π}{4}$）B．（$\sqrt{2}$，$\frac{7π}{4}$）C．（2，$\frac{π}{4}$）D．（2，$\frac{3π}{4}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

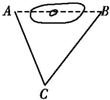    2．如图，为了测量A、B两点间的距离，在地面上选择适当的点C，测得AC=100m，BC=120m，∠ACB=60°，那么A、B的距离为（　　）
    A．20$\sqrt{91}$ mB．20$\sqrt{31}$ mC．500 mD．60$\sqrt{66}$ m

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．等比数列{an}的各项均为正数，且2a3是a2与a6的等比中项，2a1+3a2=16．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）设bn=log2a1+log2a2+…+log2an，求数列{$\frac{1}{{b}_{n}}$}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．对具有线性相关关系的变量x，y有一组观测数据（xi，yi）（i=1，2，…，8），其回归直线方程是$\widehat{y}$=$\frac{1}{3}$x+$\widehat{a}$，且x1+x2+x3+…+x8=2（y1+y2+y3+…+y8）=8，请估算x=3时，y=$\frac{7}{6}$．

    查看答案和解析>>

    同步练习册答案