
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅰ)根据题目完成![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为环保知识成绩优秀与学生的文理分类有关.
的把握认为环保知识成绩优秀与学生的文理分类有关.
(Ⅱ)现已知![]() ,
, ![]() ,
, ![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
, ![]() ,
, ![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【答案】(Ⅰ)详见解析;(Ⅱ)![]()
【解析】试题分析:(1)古典概型的概率问题,关键是正确找出基本事件总数和所求事件包含的基本事件数,然后利用古典概型的概率计算公式计算;(2)当基本事件总数较少时,用列举法把所有的基本事件一一列举出来,要做到不重不漏,有时可借助列表,树状图列举,当基本事件总数较多时,注意去分排列与组合;求随机变量的分布列的主要步骤:一是明确随机变量的取值,并确定随机变量服从何种概率分布;二是求每一个随机变量取值的概率,三是列成表格;(3)求出分布列后注意运用分布列的两条性质检验所求的分布列是否正确;(4)求解离散随机变量分布列和方差,首先要理解问题的关键,其次要准确无误的找出随机变量的所有可能值,计算出相对应的概率,写成随机变量的分布列,正确运用均值、方差公式进行计算.
试题解析:(Ⅰ)2×2列联表如下
优秀 | 非优秀 | 总计 | |
甲班 | 40 | 20 | 60 |
乙班 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由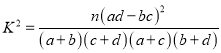 算得,
算得,
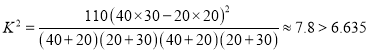 ,
,
所以有99%的把握认为学生的环保知识成绩与文理分科有关 5分
(Ⅱ)设![]() 成绩优秀分别记为事件
成绩优秀分别记为事件![]() ,则
,则![]()
∴随机变量![]() 的取值为0,1,2,3 6分
的取值为0,1,2,3 6分
![]() ,
,
![]()
![]()
![]() 10分
10分
所以随机变量![]() 的分布列为:
的分布列为:
X | 0 | 1 | 2 | 3 |
P |
E(X) =0×+1×+2×+3× = 12分


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() =2csinA
=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是89.
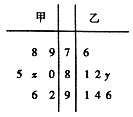
(1)求![]() 和
和![]() 的值;
的值;
(2)计算乙班7位学生成绩的方差![]() .
.
(3)从成绩在90分以上的学生中随机抽取两名学生,求乙班至少有一名学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A. 回归直线一定过样本中心![]()
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A= ![]() ,b2﹣a2=
,b2﹣a2= ![]() c2 .
c2 .
(1)求tanC的值;
(2)若△ABC的面积为3,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 是两条不同直线,
是两条不同直线, ![]() ,
, ![]() 是两个不同平面,则下列命题正确的是( )
是两个不同平面,则下列命题正确的是( )
A. 若![]() ,
, ![]() 垂直于同一平面,则
垂直于同一平面,则![]() 与
与![]() 平行
平行
B. 若![]() ,
, ![]() 平行于同一平面,则
平行于同一平面,则![]() 与
与![]() 平行
平行
C. 若![]() ,
, ![]() 不平行,则在
不平行,则在![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
D. 若![]() ,
, ![]() 不平行,则
不平行,则![]() 与
与![]() 不可能垂直于同一平面
不可能垂直于同一平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线: ![]() (
(![]() 为给定的正常数,
为给定的正常数, ![]() 为参数,
为参数, ![]() )构成的集合为
)构成的集合为![]() ,给出下列命题:
,给出下列命题:
①当![]() 时,
时, ![]() 中直线的斜率为
中直线的斜率为![]() ;
;
②![]() 中的所有直线可覆盖整个坐标平面.
中的所有直线可覆盖整个坐标平面.
③当![]() 时,存在某个定点,该定点到
时,存在某个定点,该定点到![]() 中的所有直线的距离均相等;
中的所有直线的距离均相等;
④当![]() 时,
时, ![]() 中的两条平行直线间的距离的最小值为
中的两条平行直线间的距离的最小值为![]() ;
;
其中正确的是__________(写出所有正确命题的编号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com