练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若函数f（x）=x3-ax2+1在（0，2）内单调递减，则实数a的取值范围为（ ）
    A．a≥3
    B．a=3
    C．a≤3
    D．0＜a＜3
    【答案】分析：求出导函数，令导函数小于等于0在（0，2）内恒成立，分离出参数a，求出函数的范围，得到a的范围．
    解答：解：∵函数f（x）=x3-ax2+1在（0，2）内单调递减，
    ∴f′（x）=3x2-2ax≤0在（0，2）内恒成立，
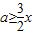
    即在（0，2）内恒成立，
    ∵，
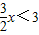
    ∴a≥3，
    故选A
    点评：解决函数在区间上的单调性已知求参数的范围的问题，递增时令导函数大于等于0恒成立；递减时，令导数小于等于0恒成立．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+
    1
    x
    ，则
     
    lim
    △x→0
    f(△x-1)+f(1)
    2△x
    等于（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+3x-1，x∈[-1，l]，则下列判断正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3+3mx2+nx+m2为奇函数，则实数m的值为
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3-3bx+b在区间（0，1）内有极小值，则b的取值范围是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若函数f（x）=x3-3x+1在闭区间[-3，0]上的最大值，最小值分别为M，m，则M+m=
    -14
    -14
    ．

    查看答案和解析>>

    同步练习册答案