练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设数列{an}的前n项和为Sn．已知S2=4,an+1=2Sn+1,n∈N*．

    (1)求通项公式an;

    (2)求数列{|an-n-2|}的前n项和．

    【答案】（1）；（2）

    【解析】分析：（1）利用与的关系可以求得通项公式；

    （2）设,,利用数列的性质进行求解。

    详解：(1)由题意得则

    又当n≥2时,由an+1-an=(2Sn+1)-(2Sn-1+1)=2an,得an+1=3an,

    所以数列{an}是以1为首项,公比为3的等比数列,所以an=3n-1,n∈N*．

    (2)设bn=|3n-1-n-2|,n∈N*,b1=2,b2=1,

    当n≥3时,由于3n-1>n+2,故bn=3n-1-n-2,n≥3,

    设数列{bn}的前n项和为Tn,则T1=2,T2=3,

    当n≥3时,Tn=3+,当n=2时,也适合上式．所以Tn=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数{an}满a1=0，an+1=an+2n，那a2016的值是（　　）
    A.2014×2015
    B.2015×2016
    C.2014×2016
    D.2015×2015

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高二学生小严利用暑假参加社会实践，为了帮助贸易公司的购物网站优化今年国庆节期间的营销策略，他对去年10月1日当天在该网站消费且消费金额不超过1000元的1000名（女性800名，男性200名）网购者，根据性别按分层抽样的方法抽取100名进行分析，得到如下统计图表（消费金额单位：元）：

    女性消费情况：

    消费金额

    （0,200）

    [200,400）

    [400,600)

    [600,800)

    [800,1000)

    人数

    5

    10

    15

    男性消费情况：

    消费金额

    （0,200）

    [200,400）

    [400,600)

    [600,800)

    [800,1000)

    人数

    2

    3

    10

    2

    （1）现从抽取的100名且消费金额在[800,1000](单位：元)的网购者中随机选出两名发放网购红包，求选出的这两名网购者恰好是一男一女的概率；

    （2）若消费金额不低于600元的网购者为“网购达人”，低于600元的网购者为“非网购达人”，根据以上统计数据填写下面列联表，并回答能否在犯错误的概率不超过0.010的前提下认为“是否为‘网购达人’与性别有关?”

    女性

    男性

    总计

    网购达人

    非网购达人

    总计

    附：

    0.10

    0.05

    0.025

    0.010

    0.005

    2.706

    3.841

    5.024

    6.635

    7.879

    （，其中）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，的部分图象如图所示．

    （Ⅰ）求函数的解析式；

    （Ⅱ）求函数的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数和满足：在区间上均有定义；函数在区间上至少有一个零点，则称和在上具有关系W．

    若，，判断和在上是否具有关系W，并说明理由；

    若和在上具有关系W，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某二手车交易市场对某型号的二手汽车的使用年数与销售价格（单位：万元/辆）进行整理，得到如下的对应数据：

    使用年数

    2

    4

    6

    8

    10

    售价

    16

    13

    9.5

    7

    4.5

    （1）试求关于的回归直线方程：（参考公式：, ．）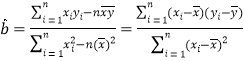

    （2）已知每辆该型号汽车的收购价格为万元，根据（1）中所求的回归方程，预测为何值时，销售一辆该型号汽车所获得的利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位： ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布．

    （1）假设生产状态正常，记表示一天内抽取的16个零件中其尺寸在之外的零件数，求及的数学期望；

    （2）一天内抽检零件中，如果出现了尺寸在之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．

    （ⅰ）试说明上述监控生产过程方法的合理性；

    （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：

    9.95

    10.12

    9.96

    9.96

    10.01

    9.92

    9.98

    10.04

    10.26

    9.91

    10.13

    10.02

    9.22

    10.04

    10.05

    9.95

    经计算得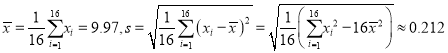，其中为

    抽取的第个零件的尺寸， ．

    用样本平均数作为的估计值，用样本标准差作为的估计值，利用估计值判断是否需对当天的生产过程进行检查？剔除之外的数据，用剩下的数据估计和（精确到0.01）．

    附：若随机变量服从正态分布，则， ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f（x）=x﹣aex（a∈R），x∈R，已知函数y=f（x）有两个零点x1 ， x2 ， 且x1＜x2 ．
    （1）求a的取值范围；
    （2）证明： 随着a的减小而增大；
    （3）证明x1+x2随着a的减小而增大．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的一元二次函数，分别从集合和中随机取一个数和得到数对．

    （1）若， ，求函数有零点的概率；

    （2）若， ，求函数在区间上是增函数的概率．

    查看答案和解析>>

    同步练习册答案