
【题目】若函数![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() 在
在![]() 上存在两个零点,求
上存在两个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)求出导函数,函数的定义域,通过①当a≤0时,②当a>0时,分别求解函数的单调区间即可;
(Ⅱ)通过a≤0时,当a>0时,利用函数的单调性结合函数的零点,列出不等式即可求解a的取值范围.
解:(Ⅰ)函数![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 单调递减.
单调递减.
当![]() 时,令
时,令![]() ,
,![]() ,其中
,其中![]() 舍去
舍去
则![]()
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
综上所述,当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
当![]() 时,所以
时,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(Ⅱ)由(Ⅰ)得,当![]() 时,
时,![]() 在
在![]() 单调递减,不合题意,舍去.
单调递减,不合题意,舍去.
当![]() 时,
时,
由于![]() 在
在![]() 上有两个零点,
上有两个零点,
又因为![]() ,所以
,所以![]() 是
是![]() 的一个零点.
的一个零点.
因此问题等价于:![]() 在
在![]() 存在一个零点,
存在一个零点,
又由(Ⅰ)得,当![]() 时,
时,![]() 存在一个极值点
存在一个极值点![]() ,
,
故![]() ,即
,即![]() .
.
因此问题等价于:
![]() .
.
因为![]()
![]() ,
,
令![]() ,
,
![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 单调递减,
单调递减,
![]() ,
,
所以![]() 成立,
成立,
所以存在![]() ,
,![]() .
.
取![]() ,
,
![]() ,
,
![]() ,
,
所以![]() 在
在![]() 存在一个零点.
存在一个零点.
综上所述,![]() .
.
另解:当![]() 趋近于
趋近于![]() 时,
时,![]() 趋近于正无穷大,则
趋近于正无穷大,则![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】现代社会,“鼠标手”已成为常见病,一次实验中,10名实验对象进行160分钟的连续鼠标点击游戏,每位实验对象完成的游戏关卡一样,鼠标点击频率平均为180次/分钟,实验研究人员测试了实验对象使用鼠标前后的握力变化,前臂表面肌电频率(![]() )等指标.
)等指标.
(I)10 名实验对象实验前、后握力(单位:![]() )测试结果如下:
)测试结果如下:
实验前:346,357,358,360,362,362,364,372,373,376
实验后:313,321,322,324,330,332,334,343,350,361
完成茎叶图,并计算实验后握力平均值比实验前握力的平均值下降了多少![]() ?
?

(Ⅱ)实验过程中测得时间![]() (分)与10名实验对象前臂表面肌电频率(
(分)与10名实验对象前臂表面肌电频率(![]() )的中的位数
)的中的位数![]() (
(![]() )的九组对应数据
)的九组对应数据![]() 为
为![]() ,
,![]() .建立
.建立![]() 关于时间
关于时间![]() 的线性回归方程;
的线性回归方程;
(Ⅲ)若肌肉肌电水平显著下降,提示肌肉明显进入疲劳状态,根据(Ⅱ)中9组数据分析,使用鼠标多少分钟就该进行休息了?
参考数据:![]() ;
;
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:


(1)求高二(1)班全体女生的人数;
(2)由频率分布直方图估计该班女生此次数学测试成绩的众数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了进行合理定价先进性试销售,其单价![]() (元)与销量
(元)与销量![]() (个)相关数据如下表:
(个)相关数据如下表:

(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性相关方程;
的线性相关方程;
(2)若该新造型糖画每个的成本为![]() 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程![]() 中斜率和截距最小二乘法估计计算公式:
中斜率和截距最小二乘法估计计算公式:

![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为F1、F2,且过点
的左、右焦点为别为F1、F2,且过点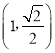 和
和 .
.

(1)求椭圆的标准方程;
(2)如图,点A为椭圆上一位于x轴上方的动点,AF2的延长线与椭圆交于点B,AO的延长线与椭圆交于点C,求△ABC面积的最大值,并写出取到最大值时直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P在曲线x2+y2=1上运动,过点P作x轴的垂线,垂足为Q,动点M满足![]() .
.
(1)求动点M的轨迹方程;
(2)点AB在直线x﹣y﹣4=0上,且AB=4,求△MAB的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com