
【题目】如图,在三棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.
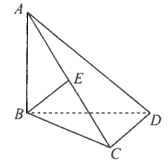
(1)证明:![]() ;
;
(2)设![]() .
.![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .求二面角
.求二面角![]() 的大小.
的大小.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某校高三男生体育课上做投篮球游戏,两人一组,每轮游戏中,每小组两人每人投篮两次,投篮投进的次数之和不少于![]() 次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为
次称为“优秀小组”.小明与小亮同一小组,小明、小亮投篮投进的概率分别为![]() .
.
(1)若![]() ,
,![]() ,则在第一轮游戏他们获“优秀小组”的概率;
,则在第一轮游戏他们获“优秀小组”的概率;
(2)若![]() 则游戏中小明小亮小组要想获得“优秀小组”次数为
则游戏中小明小亮小组要想获得“优秀小组”次数为![]() 次,则理论上至少要进行多少轮游戏才行?并求此时
次,则理论上至少要进行多少轮游戏才行?并求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
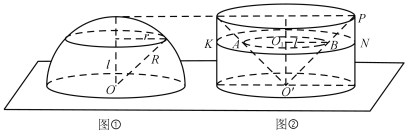
【题目】祖暅原理指出:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等,例如在计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
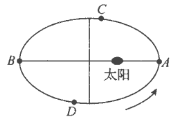
【题目】地球的公转轨道可以看作是以太阳为一个焦点的椭圆,根据开普勒行星运动第二定律,可知太阳和地球的连线在相等的时间内扫过相等的面积,某同学结合物理和地理知识得到以下结论:①地球到太阳的距离取得最小值和最大值时,地球分别位于图中![]() 点和
点和![]() 点;②已知地球公转轨道的长半轴长约为
点;②已知地球公转轨道的长半轴长约为![]() 千米,短半轴长约为
千米,短半轴长约为![]() 千米,则该椭圆的离心率约为
千米,则该椭圆的离心率约为![]() .因此该椭圆近似于圆形:③已知我国每逢春分(
.因此该椭圆近似于圆形:③已知我国每逢春分(![]() 月
月![]() 日前后)和秋分(
日前后)和秋分(![]() 月
月![]() 日前后),地球会分别运行至图中
日前后),地球会分别运行至图中![]() 点和
点和![]() 点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
点,则由此可知我国每年的夏半年(春分至秋分)比冬半年(当年秋分至次年春分)要少几天.以上结论正确的是( )
A.①B.①②C.②③D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着社会经济高速发展,人民的生活水平越来越高,部分学校安装了中央空调,某校数学建模队调查了某品牌中央空调,得到该设备使用年限x(单位:年)和维修总费用y(单位:万元)的统计表如下:(每年年底维修保养)
使用年限x(单位:年) | 2 | 3 | 4 | 5 | 6 |
维修总费用y(单位:万元) | 1 |
| 3 | 4 |
|
由上表可得线性回归方程![]() ,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
,则根据此模型预报该品牌中央空调第8年年底的维修费用约为( )
A.![]() 万元B.
万元B.![]() 万元C.
万元C.![]() 万元D.
万元D.![]() 万元
万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,
(a>b>0)的左右焦点分别为F1,F2点.M为椭圆上的一动点,△MF1F2面积的最大值为4.过点F2的直线l被椭圆截得的线段为PQ,当l⊥x轴时,![]() .
.
(1)求椭圆C的方程;
(2)过点F1作与x轴不重合的直线l,l与椭圆交于A,B两点,点A在直线![]() 上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
上的投影N与点B的连线交x轴于D点,D点的横坐标x0是否为定值?若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
⑴求椭圆![]() 的标准方程;
的标准方程;
⑵已知动直线![]() 过点
过点![]() 且与椭圆
且与椭圆![]() 交于
交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
恒成立?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com