【题目】随着社会经济高速发展，人民的生活水平越来越高，部分学校安装了中央空调，某校数学建模队调查了某品牌中央空调，得到该设备使用年限x（单位：年）和维修总费用y（单位：万元）的统计表如下：（每年年底维修保养）
使用年限x（单位：年） | 2 | 3 | 4 | 5 | 6 |
维修总费用y（单位：万元） | 1 |
| 3 | 4 |
|
由上表可得线性回归方程
，则根据此模型预报该品牌中央空调第8年年底的维修费用约为（ ）
A.
万元B.
万元C.
万元D.
万元
科目：高中数学 来源： 题型：
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况，对该公司2018年连续六个月的利润进行了统计，并根据得到的数据绘制了相应的折线图，如图所示
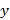
（1）由折线图可以看出，可用线性回归模型拟合月利润
（单位：百万元）与月份代码
之间的关系，求关于的线性回归方程，并预测该公司2019年3月份的利润；
（2）甲公司新研制了一款产品，需要采购一批新型材料，现有
，
两种型号的新型材料可供选择，按规定每种新型材料最多可使用
个月，但新材料的不稳定性会导致材料损坏的年限不相同，现对，两种型号的新型材料对应的产品各
件进行科学模拟测试，得到两种新型材料使用寿命的频数统计如下表：
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人，你会选择采购哪款新型材料？
参考数据：
，
.参考公式：回归直线方程为
，其中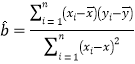
.
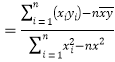查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以原点为极点，x轴的正半轴为极轴，建立极坐标系，已知曲线
的极坐标方程为
，曲线
的参数方程为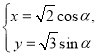
（α为参数）.设曲线与x轴、y轴的交点分别为A，B，线段
的中点为M，射线
与曲线交于点N.
（1）求曲线的普通方程与曲线的极坐标方程；
（2）求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖膈”.如图在堑堵ABC-A1B1C1中，AC⊥BC，且AA1=AB=2.下列说法正确的是（ ）
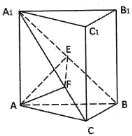
A.四棱锥B-A1ACC1为“阳马”
B.四面体A1C1CB为“鳖膈”
C.四棱锥B-A1ACC1体积最大为
D.过A点分别作AE⊥A1B于点E，AF⊥A1C于点F，则EF⊥A1B
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】张师傅欲将一球形的石材工件削砍加工成一圆柱形的新工件，已知原球形工件的半径为
，则张师傅的材料利用率的最大值等于（注：材料利用率=
）（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】设球半径为R，圆柱的体积为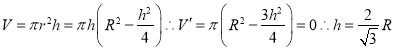
时圆柱的体积最大为
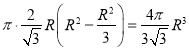,因此材料利用率=
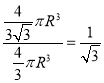,选C.
点睛:空间几何体与球接、切问题的求解方法
求解球与棱柱、棱锥的接、切问题时，一般过球心及接、切点作截面，把空间问题转化为平面图形与圆的接、切问题，再利用平面几何知识寻找几何中元素间的关系求解．
【题型】单选题
【结束】
12
【题目】已知抛物线
： 
在点
处的切线与曲线
： 
相切，若动直线
分别与曲线
、
相交于
、
两点，则
的最小值为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，抛物线C：
的焦点到直线l：
的距离为
.
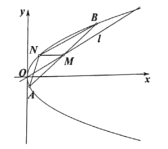
（1）求m的值.
（2）如图，已知抛物线C的动弦
的中点M在直线l上，过点M且平行于x轴的直线与抛物线C相交于点N，求
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
