
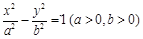 的左、右焦点分别为
的左、右焦点分别为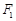 、
、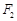 ,点
,点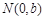 ,右顶点是M,且
,右顶点是M,且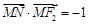 ,
,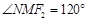 .
.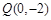 的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点
的直线l交双曲线W的右支于A、B两个不同的点(B在A、Q之间),若点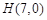 在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.
在以线段AB为直径的圆的外部,试求△AQH与△BQH面积之比λ的取值范围.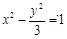 ;(2)
;(2)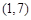 .
. ,
, 。(2)设出直线l的方程,要注意斜率存在且不为0,直线方程与双曲线方程联立利用判别式和韦达定理,点
。(2)设出直线l的方程,要注意斜率存在且不为0,直线方程与双曲线方程联立利用判别式和韦达定理,点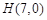 在以线段AB为直径的圆的外部,就是
在以线段AB为直径的圆的外部,就是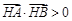 ,得
,得 ;
;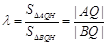 可得
可得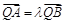 ,再转化为横坐标运算,整理得
,再转化为横坐标运算,整理得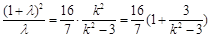 ,由
,由 求出
求出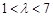 。
。 ,
,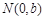 ,
,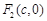 ,
,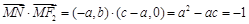 ,
,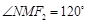 ,则
,则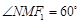 ,∴
,∴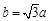 ,∴
,∴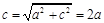 ,
, ,
, ,∴双曲线的方程为
,∴双曲线的方程为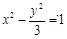 .·································· 4分
.·································· 4分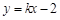 ,设
,设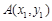 、
、 ,
,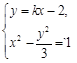 得
得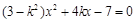 ,则
,则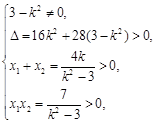
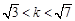 . ①································································· 6分
. ①································································· 6分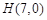 在以线段AB为直径的圆的外部,则
在以线段AB为直径的圆的外部,则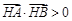 ,
,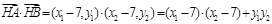
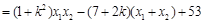
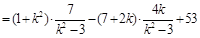
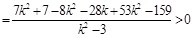 ,解得
,解得 . ②
. ② ,······················································· 8分
,······················································· 8分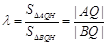 ,∵B在A、Q之间,则
,∵B在A、Q之间,则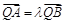 ,且
,且 ,
,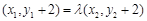 ,则
,则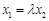 ,∴
,∴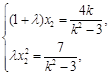
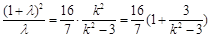 ,··················································· 10分
,··················································· 10分 ,∴
,∴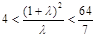 ,解得
,解得 ,又
,又 ,∴
,∴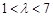 .
.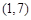 .···································································· 13分
.···································································· 13分

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com