
在△ABC中,己知 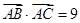 ,sinB= sinCcos
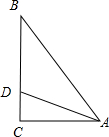
,sinB= sinCcos ,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求
,又△ABC的面积为6(Ⅰ)求△ABC的三边长;(Ⅱ)若D为BC边上的一点,且CD=1,求 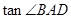 .
.
(Ⅰ) 3,4,5;(Ⅱ) 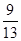
解析试题分析:(Ⅰ)由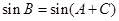 及sinB= sinCcos
及sinB= sinCcos 得sinCcos
得sinCcos =
=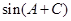 =
=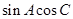
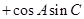 ,所以
,所以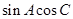 =0,因为
=0,因为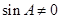 ,所以
,所以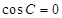 ,所以
,所以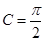 ,由平面向量数量积及三角形面积公式即可求出tanA的值,在Rt△ACB中,tanA=
,由平面向量数量积及三角形面积公式即可求出tanA的值,在Rt△ACB中,tanA= ,求出
,求出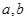 ,代入三角形面积公式求出
,代入三角形面积公式求出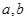 ,利用勾股定理求出c;(Ⅱ)由(Ⅰ)知tan∠BAC=
,利用勾股定理求出c;(Ⅱ)由(Ⅰ)知tan∠BAC=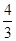 ,由三角函数定义知tan∠DAC=
,由三角函数定义知tan∠DAC= ,利用两角差的正切公式可求得tan∠BAD.
,利用两角差的正切公式可求得tan∠BAD.
试题解析:(Ⅰ)设三边分别为
∵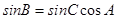 ,∴sin(A+C)=sinCcosA,
,∴sin(A+C)=sinCcosA,
化为sinAcosC+cosAsinC=sinCcosA,
∴sinAcosC=0,可得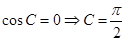
又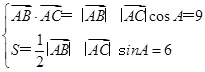
两式相除可得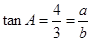
令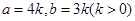
则
 三边长分别为3,4,5, (8分)
三边长分别为3,4,5, (8分)
(Ⅱ)由(Ⅰ)知tan∠BAC=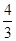 ,由三角函数定义知tan∠DAC=
,由三角函数定义知tan∠DAC= ,
,
所以tan =tan(∠BAC-∠DAC)=
=tan(∠BAC-∠DAC)=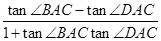 =
=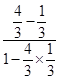 =
=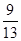 (12分)
(12分)
考点:三角变换,平面向量数量积,三角形面积公式,运算求解能力


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com