练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．已知椭圆C1比椭圆${C_2}：\frac{x^2}{12}+\frac{y^2}{16}=1$的形状更圆，则C1的离心率的取值范围是（　　）
    A．$0＜e＜\frac{1}{2}$B．$0＜e＜\frac{{\sqrt{3}}}{3}$C．$\frac{1}{2}＜e＜1$D．$\frac{{\sqrt{3}}}{3}＜e＜1$

    分析 求得椭圆C2的a，b，c，e，由椭圆的离心率的变化特点，可得椭圆C1的离心率的范围．

    解答 解：椭圆${C_2}：\frac{x^2}{12}+\frac{y^2}{16}=1$的a=4，b=2$\sqrt{3}$，
    可得c=$\sqrt{{a}^{2}-{b}^{2}}$=2，e=$\frac{c}{a}$=$\frac{1}{2}$，
    由椭圆C1比椭圆${C_2}：\frac{x^2}{12}+\frac{y^2}{16}=1$的形状更圆，
    可得C1的离心率的范围是（0，$\frac{1}{2}$）．
    故选：A．

    点评 本题考查椭圆的方程和性质，考查离心率公式的运用，以及椭圆的变化随着离心率而变，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．已知△ABC的三个顶点坐标分别为A（-1，5），B（1，-3），C（-5，4），求BC边上中线所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．若0＜θ＜$\frac{π}{2}$，化简$\frac{sinθ}{1-cosθ}$$•\sqrt{\frac{tanθ-sinθ}{tanθ+sinθ}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．若向量$\overrightarrow{a}$=（1，λ，2），$\overrightarrow{b}$=（-2，1，1），$\overrightarrow{a}$，$\overrightarrow{b}$夹角的余弦值为$\frac{1}{6}$，求λ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．已知三棱锥O-ABC中，OA=OB=2，OC=4$\sqrt{2}$，∠AOB=120°，当△AOC与△BOC的面积之和最大时，则三棱锥O-ABC的体积为$\frac{4\sqrt{6}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知椭圆E：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，F是椭圆的右焦点，点A（0，-2），若直线AF的斜率为$\frac{{2\sqrt{3}}}{3}$，O为坐标原点．
    （1）求椭圆E的方程；
    （2）过点A倾斜角为$\frac{2π}{3}$的直线l与E相交于P，Q两点，求△OPQ的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的一个焦点与抛物线y2=8x焦点相同，离心率为$\frac{1}{2}$．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）设点M（m，0）在椭圆C的长轴上，点P是椭圆上任意一点．当|$\overrightarrow{MP}$|最小时，点P恰好落在椭圆的右顶点，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{3}}{3}$，短轴长为$2\sqrt{2}$，过右焦点F的直线l与C相交于A，B两点．O为坐标原点．
    （1）求椭圆C的方程；
    （2）若点P在椭圆C上，且$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

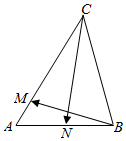    11．在△ABC中，AB=3，AC=4，N是AB的中点，M是边AC（含端点）上的动点．
    （1）若∠BAC=60°，求|$\overrightarrow{BC}$|的值；
    （2）若$\overrightarrow{BM}$⊥$\overrightarrow{CN}$，求cosA的取值范围．

    查看答案和解析>>

    同步练习册答案