
【题目】椭圆中心是原点O,它的短轴长为 ![]() ,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l:
,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l: ![]() 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)求椭圆的方程和离心率;
(2)若 ![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设 ![]() (λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明:
(λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明: ![]() .
.
【答案】
(1)解:如图,

设椭圆方程为 ![]() .
.
由|OF|=2|FA|,得c=2( ![]() ),整理得:3c2=2a2,∴e=
),整理得:3c2=2a2,∴e= ![]() .
.
联立  ,解得:a2=6,b2=2.
,解得:a2=6,b2=2.
∴椭圆的方程为 ![]() ,离心率
,离心率 ![]() .
.
(2)解:由题意可知直线l的斜率显然存在,设其斜率为k(k≠0),且A(3,0).
则直线l的方程为y=k(x﹣3),设P(x1,y1),Q(x2,y2).
联立  ,得:(1+3k2)x2﹣18k2x+27k2﹣6=0.
,得:(1+3k2)x2﹣18k2x+27k2﹣6=0.
由△=(﹣18k2)2﹣4(1+3k2)(27k2﹣6)=12(2﹣3k2)>0,得: ![]() .
.
![]() ,
, ![]() .
.
由 ![]() ,得x1x2+y1y2=0.
,得x1x2+y1y2=0.
即x1x2+(kx1﹣3k)(kx2﹣3k)= ![]()
= ![]() =0.
=0.
化简得: ![]() ,∴k=
,∴k= ![]() ,满足
,满足 ![]() .
.
(3)解: ![]() ,
, ![]() ,
,
由已知得方程组  ,解得:
,解得: ![]() .
.
∵F(2,0),M(x1,﹣y1).
故 ![]() =(λ(x2﹣3)+1,﹣y1)
=(λ(x2﹣3)+1,﹣y1)
= ![]() =
= ![]() .
.
而 ![]() .
.
∴ ![]() .
.
【解析】(1)首先由条件|OF|=2|FA|列式,求出椭圆的离心率,然后结合短轴长2b= ![]() 及a2=b2+c2可求a2 , 则椭圆方程可求;(2)写出过点A的直线方程,设出直线与椭圆相交于P、Q两点的坐标,联立直线方程和椭圆方程后求出P、Q两点的横坐标的和与积,由
及a2=b2+c2可求a2 , 则椭圆方程可求;(2)写出过点A的直线方程,设出直线与椭圆相交于P、Q两点的坐标,联立直线方程和椭圆方程后求出P、Q两点的横坐标的和与积,由 ![]() ,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;(3)由向量的坐标表示写出
,得到P、Q两点的坐标的关系,转化为横坐标的关系后,把前面得到的和与积的表达式代入即可求出直线的斜率,则直线方程可求;(3)由向量的坐标表示写出 ![]() ,
, ![]() ,再由
,再由 ![]() (λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.
(λ>1)及P,Q两点的坐标都适合椭圆方程列式找出P,Q两点的坐标与λ的关系,最后把要证的等式的两边的坐标都用λ和纵坐标表示即可得证.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,且anan+1+an+1﹣2an=0(n∈N+).
(1)求a2、a3、a4的值;
(2)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(用空间向量坐标表示解答)已知正三棱柱ABC﹣A1B1C1的各棱长都是4,E是BC的中点,F在CC1上,且CF=1. 
(1)求证:EF⊥A1C;
(2)求二面角C﹣AF﹣E的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为 ![]() 元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为
元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为 ![]() 元(k为正常数).
元(k为正常数).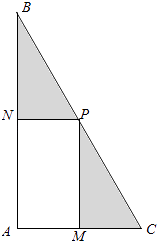
(1)试用x表示S,并求S的取值范围;
(2)求总造价T关于面积S的函数T=f(S);
(3)如何选取|AM|,使总造价T最低(不要求求出最低造价).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|x2+4x=0,x∈R},B={x|x2+2(a+1)x+a2﹣1=0,x∈R},
(1)若A∩B=A∪B,求实数a的值;
(2)若A∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣t|+ ![]() (x>0);
(x>0);
(1)判断函数y=f(x)在区间(0,t]上的单调性,并证明;
(2)若函数y=f(x)的最小值为与t无关的常数,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com