
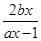 ,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.
,a≠0,f(1)=1,且使f(x)=2x成立的实数x只有一个.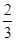 ,an+1=f(an),bn=
,an+1=f(an),bn=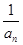 -1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式;
-1,n∈N*,证明数列{bn}是等比数列,并求出{bn}的通项公式; . (2)bn=b1qn-1=
. (2)bn=b1qn-1=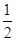
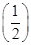 n-1=
n-1=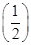 n(n∈N*).
n(n∈N*).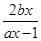 ,f(1)=1,得a=2b+1.
,f(1)=1,得a=2b+1.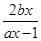 =2x,
=2x, .…………………………………………4分
.…………………………………………4分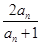 (n∈N*),bn=
(n∈N*),bn=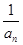 -1, ∴
-1, ∴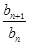 =
=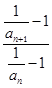 =
=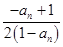 =
=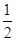 ,
,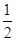 .又∵a1=
.又∵a1=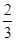 ,∴b1=
,∴b1=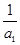 -1=
-1=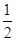 ,
,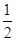
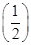 n-1=
n-1=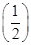 n(n∈N*).……………………………9分
n(n∈N*).……………………………9分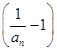 =1-an=1-
=1-an=1-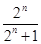 =
=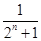 ,
, 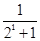 +
+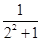 +…+
+…+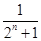 <
<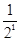 +
+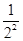 +…+
+…+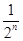
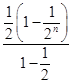 =1-
=1-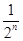 <1(n∈N*).
<1(n∈N*).

科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 米,宽
米,宽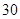 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔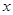 米(
米( ,
,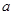 为正常数)需打建一个桩位,每个桩位需花费
为正常数)需打建一个桩位,每个桩位需花费 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的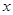 米墙面需花
米墙面需花 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当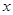 为何值时,所需总费用最少?
为何值时,所需总费用最少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 与时间
与时间 的关系,可近似地表示为
的关系,可近似地表示为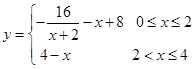 。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。
。只有当河流中碱的浓度不低于1时,才能对污染产生有效的抑制作用。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com