
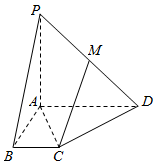
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.分析 (I)取PA中点N,则可证明四边形BCMN是平行四边形,故而CM∥BN,于是CM∥平面PAB;
(II)利用平面几何知识,证明CD⊥AC,又PA⊥平面ABCD,故PA⊥CD,于是CD⊥平面PAC;
(III)当E为AD中点时,可证BC⊥CE,ME⊥BC,故而BC⊥平面MCE,于是MCE⊥平面PBC.
解答 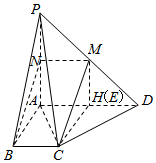 证明:(I)取PA的中点N,连接MN、BN,
证明:(I)取PA的中点N,连接MN、BN,
则MN∥AD,MN=$\frac{1}{2}$AD,
又∵BC∥AD,BC=$\frac{1}{2}AD$,
∴MN∥BC,MN=BC,
∴四边形BCMN为平行四边形,
∴BN∥CM,
又∵BN?平面PAB,CM?平面PAB,
∴CM∥平面PAB.
(II)在梯形ABCD中,AB=BC=1,AD=2,∠BAD=90°
过C作CH⊥AD于H,则CH=AB=1,AH=BC=1,
∴DH=1.AC=CD=$\sqrt{2}$.
∵AC2+CD2=AD2,∴CD⊥AC.
又∵PA⊥平面ABCD,CD?平面ABCD,
∴CD⊥PA.
∵PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴CD⊥平面PAC.
(III)当E为AD的中点时,平面MCE⊥平面PBC.
由(II)可知H为AD的中点,此时E与H重合.连结ME,
∵M,E分别是PD,AD的中点,
∴ME∥PA,∵PA⊥平面ABCD,
∴ME⊥平面ABCD,∵BC?平面ABCD,
∴BC⊥ME,又∵BC⊥CE,CE?平面MCE,ME?平面MCE,CE∩ME=E,
∴BC⊥平面MCE,∵BC?平面PBC,
∴平面MCE⊥平面PBC.
点评 本题考查了线面平行,线面垂直,面面垂直的判定,构造平行线与垂线是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x+1)(x-5)<0 | B. | (x-1)(x+5)<0 | C. | (x-1)(x+5)>0 | D. | (x+1)(x-5)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,-家电商根据以往某种热销产品的销售记录,绘制了这种商品日销售的频率分布直方图,若-个月以30天计算,估计该家电商一个月内这种商品日销售不少于150个的天数9.
如图所示,-家电商根据以往某种热销产品的销售记录,绘制了这种商品日销售的频率分布直方图,若-个月以30天计算,估计该家电商一个月内这种商品日销售不少于150个的天数9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com