
分析 (1)不等式即 x2-2x+3<|x-2|,且x≠2,分类讨论去掉绝对值,求得x的范围.
(2)不等式即 x2+x+1>|x-2|•(2x+1),分类讨论去掉绝对值,求得x的范围.
解答 解:(1)∵|$\frac{{x}^{2}-2x+3}{x-2}$|<1,x2-2x+3=(x-1)2+2>0,
∴不等式即 x2-2x+3<|x-2|,且x≠2.
当x>2时,x2-2x+3<x-2,x2-3x+5<0,x无解.
当x<2时,x2-2x+3<-x+2,x2-x+1<0,求得x无解.
综上,原不等式的解集为∅.
(2)对于|$\frac{{x}^{2}+x+1}{x-2}$|>2x+1,∵x2+x+1>0,x≠2.
∴不等式即 x2+x+1>|x-2|•(2x+1).
∴$\left\{\begin{array}{l}{x-2>0}\\{{x}^{2}+x+1>(x-2)(2x+1)}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{x-2<0}\\{{x}^{2}+x+1>(2-x)(2x+1)}\end{array}\right.$②.
解①可得2<x<1+$\sqrt{7}$;解②可得x<-$\frac{1}{3}$,或1<x<2.
综上可得,不等式的解集为{2<x<1+$\sqrt{7}$ 或x<-$\frac{1}{3}$,或1<x<2}.
点评 本题主要考查分式不等式、绝对值不等式的解法,体现了转化的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.
如图,在四棱锥P-ABCD中,底面四边形ABCD内接于圆O,AC是圆O的一条直径,PA⊥平面ABCD,E是PC的中点,∠DAC=∠AOB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在圆外 | B. | 在圆上 | C. | 在圆内 | D. | 无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
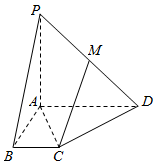 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥BC,BC∥AD,AB=BC=1,AD=2,M为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90元 | B. | 45元 | C. | 55元 | D. | 60.82元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com