
已知椭圆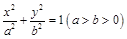 上一点
上一点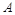 关于原点的对称点为
关于原点的对称点为 为其右焦点,若
为其右焦点,若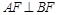 ,设
,设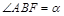 ,且
,且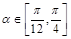 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .
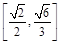
解析试题分析:∵B和A关于原点对称,∴B也在椭圆上。
设左焦点为F′,根据椭圆定义:|AF|+|AF′|=2a
又∵|BF|=|AF′| ∴|AF|+|BF|=2a ……①
O是Rt△ABF的斜边中点,∴|AB|=2c
又|AF|=2csinα ……②
|BF|=2ccosα ……③
将②③代入① 2csinα+2ccosα=2a
∴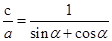 ,即
,即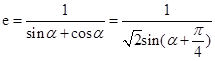 ,
,
∵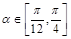 ,
,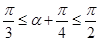
∴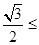
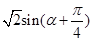 )≤1,故椭圆离心率的取值范围为
)≤1,故椭圆离心率的取值范围为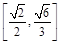 。
。
考点:本题主要考查椭圆的定义及其几何性质,两角和的正弦公式,正弦函数的图象和性质。
点评:中档题,本题利用椭圆的定义及直角三角形中的边角关系,确定得到了椭圆离心率的表达式,根据角的范围确定离心率的范围,该题综合性较强,也较为典型。


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:填空题
已知有公共焦点的椭圆与双曲线中心在原点,焦点在x轴上,左、右焦点分别为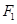 ,
,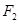 ,且它们在第一象限的交点为P,△
,且它们在第一象限的交点为P,△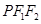 是以
是以 为底边的等腰三角形.若
为底边的等腰三角形.若 =10,双曲线的离心率的取值范围为(1,2),则该椭圆的离心率的取值范围是
=10,双曲线的离心率的取值范围为(1,2),则该椭圆的离心率的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
我们把形如 的函数称为“莫言函数”,并把其与
的函数称为“莫言函数”,并把其与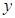 轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当
轴的交点关于原点的对称点称为“莫言点”,以“莫言点”为圆心凡是与“莫言函数”图象有公共点的圆,皆称之为“莫言圆”.当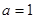 ,
,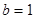 时,在所有的“莫言圆”中,面积的最小值 .
时,在所有的“莫言圆”中,面积的最小值 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com