
分析 (1)根据向量的数量级的定义计算cosθ;
(2)计算(3$\overrightarrow{a}+5\overrightarrow{b}$)2,然后开方即可得到|3$\overrightarrow{a}-5\overrightarrow{b}$|;
(3)令(3$\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$-$\overrightarrow{b}$)=0列方程解出k.
解答 解:(1)∵$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=cos$θ=-\frac{1}{2}$,
∴$θ=\frac{2π}{3}$.
(2)(3$\overrightarrow{a}+5\overrightarrow{b}$)2=9${\overrightarrow{a}}^{2}+30\overrightarrow{a}•\overrightarrow{b}+25{\overrightarrow{b}}^{2}$=9-15+25=19,
∴|3$\overrightarrow{a}$+5$\overrightarrow{b}$|=$\sqrt{19}$.
(3)∵(3$\overrightarrow{a}$+k$\overrightarrow{b}$)⊥(k$\overrightarrow{a}$-$\overrightarrow{b}$),∴(3$\overrightarrow{a}$+k$\overrightarrow{b}$)•(k$\overrightarrow{a}$-$\overrightarrow{b}$)=0,
即3k${\overrightarrow{a}}^{2}$+(k2-3)$\overrightarrow{a}•\overrightarrow{b}$-k${\overrightarrow{b}}^{2}$=0,
∴3k-$\frac{1}{2}$(k2-3)-k=0,
解得k=2+$\sqrt{7}$或k=2-$\sqrt{7}$.
点评 本题考查了平面向量的数量级运算,向量垂直与数量级的关系,属于基础题.


科目:高中数学 来源: 题型:选择题
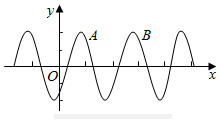 已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$).则下列说法错误的是( )
已知函数f(x)=2cos(ωx-φ)(ω>0,φ∈[0,π])的部分图象如图所示,若A($\frac{π}{2}$,$\sqrt{2}$),B($\frac{3π}{2}$,$\sqrt{2}$).则下列说法错误的是( )| A. | φ=$\frac{3π}{4}$ | |
| B. | 函数f(x)的一条对称轴为x=$\frac{15π}{8}$ | |
| C. | 为了得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移$\frac{π}{8}$个单位 | |
| D. | 函数f(x)的一个单调减区间为[$\frac{9π}{8}$,$\frac{13π}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
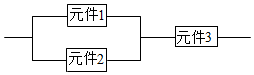 某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.
某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com