
分析 (1)设N(4,y0),代入x2=2py,结合|NF|=$\frac{5}{4}$|MN|,求出p,即可求解C的方程.
(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y=$\frac{t-1}{2}$x+t,直线PB的方程是y=$\frac{1-t}{2}$x+t分类讨论:①当-1<t<0时,l∥PA,不符合题意;②当t≤-1时,$\frac{t-1}{2}$≤-1<$\frac{m}{2}$,$\frac{1-t}{2}$≥1>$\frac{m}{2}$,分别联立方程组,解得D,E的横坐标,进而可得△QAB与△PDE的面积之比,利用其为常数,即可求得结论.
解答 解:(1)设N(4,y0),代入x2=2py,得y0=$\frac{8}{p}$,
∴|MN|=$\frac{8}{p}$,|NF|=$\frac{p}{2}$+$\frac{8}{p}$.
由题设|NF|=$\frac{5}{4}$|MN|,
得$\frac{p}{2}$+$\frac{8}{p}$=$\frac{5}{4}$×$\frac{8}{p}$,解得p=-2(舍去)或p=2,
∴C的方程为x2=4y;
(2)假设存在点P(0,t)(t<0),满足条件,则直线PA的方程是y=$\frac{t-1}{2}$x+t,直线PB的方程是y=$\frac{1-t}{2}$x+t.
∵-2<m<2,∴-1<$\frac{m}{2}$<1
①当-1<t<0时,-1<$\frac{t-1}{2}$<-$\frac{1}{2}$,存在m∈(-2,2),使得$\frac{m}{2}$=$\frac{t-1}{2}$.
∴l∥PA,∴当-1<t<0时,不符合题意;
②当t≤-1时,$\frac{t-1}{2}$≤-1<$\frac{m}{2}$,$\frac{1-t}{2}$≥1>$\frac{m}{2}$,
∴l与直线PA,PB一定相交,分别联立方程组$\left\{\begin{array}{l}{y=\frac{t-1}{2}x+t}\\{y=\frac{m}{2}x-\frac{{m}^{2}}{4}}\end{array}\right.$,$\left\{\begin{array}{l}{y=\frac{1-t}{2}x+t}\\{y=\frac{m}{2}x-\frac{{m}^{2}}{4}}\end{array}\right.$,
解得D,E的横坐标分别是xD=$\frac{{m}^{2}+4t}{2(m+1-t)}$,xE=$\frac{{m}^{2}+4t}{2(m+t-1)}$.
∴xE-xD=$(1-t)•\frac{{m}^{2}+4t}{{m}^{2}-(t-1)^{2}}$
∵|FP|=-$\frac{{m}^{2}}{4}$-t
∴S△PDE=$\frac{1}{2}|FP|×$|xE-xD|=$\frac{t-1}{8}×$$\frac{({m}^{2}+4t)^{2}}{{m}^{2}-(t-1)^{2}}$
∵S△QAB=$\frac{4-{m}^{2}}{2}$
∴$\frac{{S}_{△QAB}}{{S}_{△PDE}}$=$\frac{4}{1-t}×\frac{{m}^{4}-[4+(t-1)^{2}]{m}^{2}+4(t-1)^{2}}{{m}^{4}+8t{m}^{2}+16{t}^{2}}$
∵x0∈(-2,2),△QAB与△PDE的面积之比是常数
∴$\left\{\begin{array}{l}{-4-(t-1)^{2}=8t}\\{4(t-1)^{2}=16{t}^{2}}\end{array}\right.$,解得t=-1,
∴△QAB与△PDE的面积之比是2.
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系的综合应用,考查向量知识的运用,考查分类讨论的数学思想,考查三角形面积的计算,同时考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
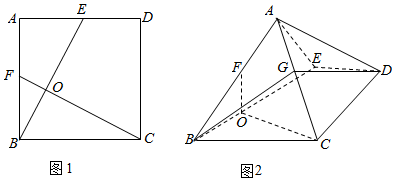 如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点
如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com