
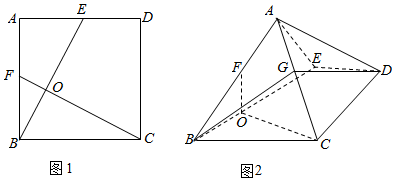
 如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点
如图1已知正方形ABCD的边长为2,E,F分别为边AD、AB的中点,将△ABE沿BE折起,使平面ABE⊥平面BCDE,如图2,点G为AC的中点分析 (I)连结EF,FG,则可证四边形EFGD是平行四边形,故GD∥EF,从而GD∥平面ABE;
(II)利用等面积法求出Rt△ABE斜边上的高h,则h为三棱锥A-BDE的高,于是VG-ABE=VD-ABE=VA-BDE.
解答 证明:(I连结EF,FG,
∵F,G分别是AB,AC的中点,
∴FG∥BC,FG=$\frac{1}{2}BC$,
又在图1中,四边形ABCD是正方形,E是AD的中点,
∴DE∥BC,DE=$\frac{1}{2}$BC,
∴四边形DEFG是平行四边形,
∴DG∥EF,又DG?平面ABE,EF?平面ABE,
∴DG∥平面ABE.
解:(II)∵DG∥平面ABE,
∴VG-ABE=VD-ABE=VA-BDE.
∵AB=2,AE=1,∴BE=$\sqrt{5}$,
∴Rt△ABE的斜边BE上的高h=$\frac{AB•AE}{BE}=\frac{2\sqrt{5}}{5}$.
∵平面ABE⊥平面BCDE,
∴A到平面BCDE的距离d=h=$\frac{2\sqrt{5}}{5}$.
∴VA-BDE=$\frac{1}{3}{S}_{△BDE}•h$=$\frac{1}{3}×\frac{1}{2}×1×2×\frac{2\sqrt{5}}{5}$=$\frac{2\sqrt{5}}{15}$.
点评 本题考查了线面平行的判定,面面垂直的性质,棱锥的体积计算,属于中档题.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∨(¬q)是假命题 | D. | 命题p∧(¬q)是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,G、F分别为EO、EB中点,且AB=$\sqrt{2}$CE.
在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,G、F分别为EO、EB中点,且AB=$\sqrt{2}$CE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{{\sqrt{7}}}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
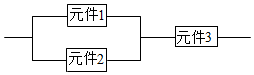 某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.
某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1200,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1200小时的概率为$\frac{3}{8}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com