
 如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π.
如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π. 分析 由题意,确定四边形ABQC的外接圆的直径为4,P-ABQC外接球的球心在过O点,且垂直于圆O所在平面的直线l上,在Rt△AOO′中,利用勾股定理求出R,即可求出P-ABQC外接球的表面积.
解答 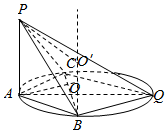 解:∵AC=2,Q是圆O上的动点,∠AQC=30°,
解:∵AC=2,Q是圆O上的动点,∠AQC=30°,
∴四边形ABQC的外接圆的直径为4.
由题意,P-ABQC外接球的球心在过O点,且垂直于圆O所在平面的直线l上,
则l∥PA,
设球心为O′,外接圆的半径为R,故O′A=O′P=R,且OO′=$\frac{1}{2}$PA=2.
在Rt△AOO′中,R2=22+22=8,
所以P-ABQC外接球的表面积为4πR2=32π.
故答案为:32π.
点评 本题考查P-ABQC外接球的表面积,考查学生的计算能力,确定球心与半径是关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
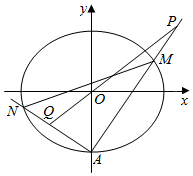 在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,连接椭圆C的四个顶点所形成的四边形面积为4$\sqrt{3}$.
在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,连接椭圆C的四个顶点所形成的四边形面积为4$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
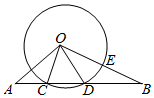 如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,OB与⊙O相交于点E,AC=4,CD=3,∠BOD=∠A,则BE=( )
如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,OB与⊙O相交于点E,AC=4,CD=3,∠BOD=∠A,则BE=( )| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
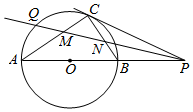 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 线性回归直线一定过点(4.5,3.5) | |
| B. | 产品的生产能耗与产量呈正相关 | |
| C. | t的取值必定是3.15 | |
| D. | A产品每多生产1吨,则相应的生产能耗约增加0.7吨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com