
分析 (Ⅰ)求出f(x)的导数,根据x的范围,判断出f′(x)的符号,从而求出函数的单调性;
(Ⅱ)问题转化为证明${e^{2x+1}}>2\sqrt{2}sin(x+\frac{π}{4})$,在$?x∈[{-1,\frac{1}{2}}]$上恒成立,构造函数$g(x)=2x+2-2\sqrt{2}sin(x+\frac{π}{4})$,$x∈[{-1,\frac{1}{2}}]$,求出g(x)的导数,判断出函数的单调性,从而证出结论.
解答 解:(I)由题f'(x)=-e1-x(cosx)-e1-xsinx=-e1-x(sinx+cosx)…(2分)
因为$x∈(0,\frac{π}{2})$
所以f'(x)<0…(3分)
所以函数f(x)在$(0,\frac{π}{2})$上单调递减…(4分)
(II)f(-x-1)=ex+2•cos(-x-1)=ex+2•cos(x+1).
而2f'(x)•cos(x+1)=-2e1-x(sinx+cosx)•cos(x+1),…(5分)
又因为$?x∈[{-1,\frac{1}{2}}]$,所以cos(x+1)>0.…(6分)
要证原不等式成立,只要证ex+2-2e1-x(sinx+cosx)>0,
只要证ex+2>2e1-x(sinx+cosx),
只要证${e^{2x+1}}>2\sqrt{2}sin(x+\frac{π}{4})$,在$?x∈[{-1,\frac{1}{2}}]$上恒成立.…(7分)
首先构造函数$g(x)=2x+2-2\sqrt{2}sin(x+\frac{π}{4})$,$x∈[{-1,\frac{1}{2}}]$,
因为$g'(x)=2-2\sqrt{2}cos(x+\frac{π}{4})$=$2\sqrt{2}(\frac{{\sqrt{2}}}{2}-cos(x+\frac{π}{4}))$,
可得,在x∈[-1,0]时,g'(x)≤0,即g(x)在[-1,0]上是减函数,
在$x∈({0,\frac{1}{2}}]$时,g'(x)>0,即g(x)在$({0,\frac{1}{2}}]$上是增函数,…(8分)
所以,在$[{-1,\frac{1}{2}}]$上,g(x)min=g(0)=0,所以g(x)≥0.
所以,$2\sqrt{2}sin(x+\frac{π}{4})≤2x+2$,等号成立当且仅当x=0时.…(10分)
其次构造函数h(x)=e2x+1-(2x+2),$x∈[{-1,\frac{1}{2}}]$,
因为h'(x)=2e2x+1-2=2(e2x+1-1),
可见$x∈[{-1,-\frac{1}{2}}]$时,h'(x)≤0,即h(x)在$[{-1,-\frac{1}{2}}]$上是减函数,
$x∈({-\frac{1}{2},\frac{1}{2}}]$时,h'(x)>0,即h(x)在$({-\frac{1}{2},\frac{1}{2}}]$上是增函数,
所以在$[{-1,\frac{1}{2}}]$上,$h{(x)_{min}}=h(-\frac{1}{2})=0$,所以h(x)≥0,
所以,e2x+1≥2x+2,等号成立当且仅当$x=-\frac{1}{2}$时.…(11分)
综上所述,${e^{2x+1}}≥2x+2≥2\sqrt{2}sin(x+\frac{π}{4})$,
因为取等条件并不一致,
所以${e^{2x+1}}>2\sqrt{2}sin(x+\frac{π}{4})$,在$?x∈[{-1,\frac{1}{2}}]$上恒成立,
所以$?x∈[{-1,\frac{1}{2}}]$,总有f(-x-1)+2f'(x)•cos(x+1)>0成立.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,不等式的证明、函数的构造,是一道综合题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
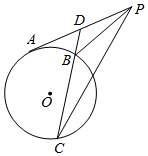 如图,已知PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.PD=2,PB=3,$DB=\frac{3}{2}$,则PC=4.
如图,已知PA切⊙O于点A,D为PA的中点,过点D引割线交⊙O于B、C两点.PD=2,PB=3,$DB=\frac{3}{2}$,则PC=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π.
如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
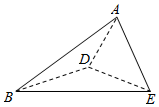 已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )
已知三棱锥A-BCD中,△ACD为等边三角形,且平面ACD⊥平面BCD,BD⊥CD,BD=CD=2,则三棱锥A-BCD外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}$π | C. | 8π | D. | $\frac{28}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b | B. | a<b | C. | a+b=1 | D. | a+b<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com