
分析 先求出A(0,2),直线为x-y-2=0,由此利用点到直线的距离公式能求出点A(2,$\frac{π}{2}$)到直线ρcos($θ+\frac{π}{4}$)=$\sqrt{2}$的距离.
解答 解:在极坐标系中,点A(2,$\frac{π}{2}$),
∴在平面直角坐标系中,A(2cos$\frac{π}{2}$,2sin$\frac{π}{2}$),即A(0,2),
∵ρcos($θ+\frac{π}{4}$)=ρ(cos$θcos\frac{π}{4}$-sin$θsin\frac{π}{4}$)=$\frac{\sqrt{2}}{2}ρ$cosθ-$\frac{\sqrt{2}}{2}ρ$sinθ=$\sqrt{2}$,
∴$\frac{ρ}{2}cosθ-\frac{ρ}{2}sinθ$=1,
∴ρcosθ=x,ρsinθ=y,
∴直线为x-y-2=0,
点A(0,2)到直线x-y-2=0的距离:d=$\frac{|0-2-2|}{\sqrt{2}}$=2$\sqrt{2}$,
∴点A(2,$\frac{π}{2}$)到直线ρcos($θ+\frac{π}{4}$)=$\sqrt{2}$的距离为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查点到直线的距离的求法,是基础题,解题时要认真审题,注意极坐标和直角坐标的相互转化.


科目:高中数学 来源: 题型:解答题
 在直三棱锥ABC-A1B1C1中,AA1=AB=AC=2,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.
在直三棱锥ABC-A1B1C1中,AA1=AB=AC=2,E,F分别是CC1,BC的中点,AE⊥A1B1,D为棱A1B1上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
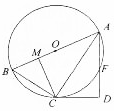 如图,AB是圆O的直径,C,F是圆O上的点,CA平分∠BAF,过C点作圆O的切线交AF的延长线于D点,CM⊥AB,垂足为M.
如图,AB是圆O的直径,C,F是圆O上的点,CA平分∠BAF,过C点作圆O的切线交AF的延长线于D点,CM⊥AB,垂足为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
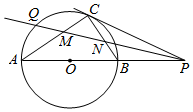 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示.
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示. | P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 晕机 | 不晕机 | 合计 | |
| 女 | 10 | 20 | 30 |
| 男 | 10 | 70 | 80 |
| 合计 | 20 | 90 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com