
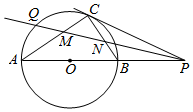
 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:分析 (1)根据题意,证明∠CNM=∠CMN,即可证明△CMN是等腰三角形;
(2)利用对应角相等证明△PNB∽△PMC,即可证明PB•CM=PC•BN.
解答 解:(1)∵PC是圆O的切线,切点为C,
∴∠PCB=∠PAC;
又∵∠CPM=∠APM,
∴∠CNM=∠CPM+∠PCB=∠APM+∠PAM=∠CMN,
∴△CMN是等腰三角形;
(2)∵∠CMN=∠CNM,∠CNM=∠BNP,
∴∠CMN=∠BNP,
又∵∠CNP=∠BPN,
∴△PNB∽△PMC,
∴$\frac{PB}{PC}$=$\frac{BN}{CM}$,
即PB•CM=PC•BN.
点评 本题考查了推理与证明的应用问题,也考查了圆与三角形的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
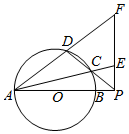 如图,圆O的直径AB=4,P是AB延长线上一点,BP=1,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
如图,圆O的直径AB=4,P是AB延长线上一点,BP=1,割线PCD交圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π.
如图,圆O是△ABC的外接圆,PA垂直圆O所在的平面,PA=4,AC=2,Q是圆O上的动点,∠AQC=30°,则四棱锥P-ABQC外接球的表面积为32π.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱网购 | 不喜爱网购 | 合计 | |
| 女 | 20 | 5 | 25 |
| 男 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com