
分析 (1)令n=2、1依次代入递推公式列出方程,求出a2、a1的值;
(2)根据条件分两种情况:当p=0,q≠0时由数列的递推公式对n分奇数和偶数求出Sn;当p≠0,q=0时由数列的递推公式可知是等比数列,根据等比数列的前n项和公式求出Sn;
(3)由题意求出数列的递推公式,由p的范围先比较a1与a2,令n取n-1列出式子后,两式相减化简后利用基本不等式求出an的范围,根据p的范围判断出“an+1-an”的符号,即可证明结论.
解答 解:(1)由题意知,an+1=p•an+$\frac{q}{a_n}$,∴a3=p•a2+$\frac{q}{{a}_{2}}$,
∵p=$\frac{1}{2}$,q=2,且a3=$\frac{41}{20}$,∴$\frac{41}{20}=\frac{1}{2}({a}_{2}+\frac{4}{{a}_{2}})$,解得${a}_{2}=\frac{5}{2}或{a}_{2}=\frac{8}{5}$,…2分
当${a_2}=\frac{5}{2}$时,同理求得a1=1或4;当${a_2}=\frac{8}{5}$时,无解,
所以,a1=1或4 …4分
(2)若p=0,q≠0,${a_{n+1}}=\frac{q}{a_n}$,∴${a_1}=5,{a_2}=\frac{q}{5},{a_3}=5,{a_4}=\frac{q}{5}$,…5分
所以当n为奇数时,${S_n}=5•\frac{n-1}{2}+\frac{q}{5}•\frac{n+1}{2}=\frac{25n+qn+q-25}{10}$;…6分
当n为偶数时,${S_n}=5•\frac{n}{2}+\frac{q}{5}•\frac{n}{2}=\frac{25n+qn}{10}$,
所以${S}_{n}=\left\{\begin{array}{l}{\frac{25n+qn+q-25}{10},n为奇数}\\{\frac{25n+qn}{10},n为偶数}\end{array}\right.$…7分
若p≠0,q=0时,an+1=p•an,…8分
所以${S_n}=\left\{{\begin{array}{l}{\frac{{5({p^n}-1)}}{p-1}}&{p≠0,p≠1}\\{5n}&{p=1}\end{array}}\right.$…10分
证明:(3)由题意知,$\left\{{\begin{array}{l}{{a_1}=1}\\{{a_{n+1}}=p•{a_n}+\frac{1}{a_n}}\end{array}}\right.$
当$p<\frac{3}{4}$时,可得${a_2}=2p+\frac{1}{2}<2={a_1}$ ①…12分
由${a_{n+1}}=p•{a_n}+\frac{1}{a_n}$和${a_n}=p•{a_{n-1}}+\frac{1}{{{a_{n-1}}}},(n≥2)$,
两式相减得,${a_{n+1}}-{a_n}=({a_n}-{a_{n-1}})(p-\frac{1}{{{a_n}{a_{n-1}}}})$ …14分
因为${a_n}=p•{a_{n-1}}+\frac{1}{{{a_{n-1}}}}≥2\sqrt{p}$成立,则有an•an-1>4p
当$p>\frac{1}{2}$时,${a_n}•{a_{n-1}}>4p>\frac{1}{p}$,即$p>\frac{1}{{{a_n}{a_{n-1}}}}$ ②…16分
由①②可知,当an<an-1时,恒有an+1<an…17分
对于任意的自然数n,an+1<an恒成立. …18分.
点评 本题考查了数列递推关系,等比数列的定义、前n项和公式,作差法判断数列的单调性,以及基本不等式式的应用,考查了分类讨论方法、推理能力与化简、变形能力,属于难题.


科目:高中数学 来源: 题型:解答题
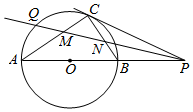 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 线性回归直线一定过点(4.5,3.5) | |
| B. | 产品的生产能耗与产量呈正相关 | |
| C. | t的取值必定是3.15 | |
| D. | A产品每多生产1吨,则相应的生产能耗约增加0.7吨 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $-\frac{1}{6}$ | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com