
分析 (1)先根据导数乘法的运算法则求出函数的导函数,然后讨论f'(x)=0时两根大小,然后分别解不等式f'(x)<0与f'(x)>0,从而求出函数的单调区间;
(2)由(1)知,当a>0时,f(x)在区间[0,4]上的单调性,从而求出函数f(x)在区间[0,4]上的值域,根据g(x)在[0,4]上单调递增,可求出g(x)在[0,4]的值域;
若存在(a>0),x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,只需要gmin(x)-fmax(x)<1,解不等式即可.
解答 .解:(1)f'(x)=-[x2+(a-2)x-3a-3]e3-x=-(x-3)(x+a+1)e3-x
由-a-1=3得a=-4,
当a=-4时,f′(x)=-(x-3)2e3-x≤0,此时函数在(-∞,+∞)上为减函数,
当a<-4时,-a-1>3,由f'(x)<0⇒x<3或x>-a-1,f'(x)>0⇒3<x<-a-1.
∴f(x)单调减区间为(-∞,3),(-a-1,+∞),单调增区间为(3,-a-1).
当a>-4时,-a-1<3,
f'(x)<0⇒x>3或x<-a-1,f'(x)>0⇒-a-1<x<3.
∴f(x)单调减区间为(-∞,-a-1),(3,+∞),单调增区间为(-a-1,3).
(2)由(1)知,当a>0时,-a-1<0,f(x)在区间[0,3]上的单调递增,
在区间[3,4)]单调递减,而f(0)=-(2a+3)e3<0,f(4)=(2a+13)e-1>0,f(3)=a+6.
那么f(x)在区间[0,4]上的值域是F=[-(2a+3)e3,a+6]
又g(x)=(a2+$\frac{25}{4}$)ex(a>0),在[0,4]上是增函数,对应的值域为G=[a2+$\frac{25}{4}$,(a2+$\frac{25}{4}$)e4],
∵a>0,∴-(2a+3)e3<a+6≤a2+$\frac{25}{4}$<(a2+$\frac{25}{4}$)e4,
|f(x1)-g(x2)|<1等价为g(x2)-f(x1)<1
若存在(a>0),x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,
只需要gmin(x)-fmax(x)<1,
∴a2+$\frac{25}{4}$-a-6<1,得4a2-4a-3<0,得-$\frac{1}{2}$<a<$\frac{3}{2}$
∵a>0,
∴0<a<$\frac{3}{2}$
∴a的取值范围为(0,$\frac{3}{2}$).
点评 本题主要考查了利用导数求闭区间上函数的最值,以及利用导数研究函数的单调性,同时考查了分类讨论的数学思想,综合性较强,难度较大.


科目:高中数学 来源: 题型:解答题
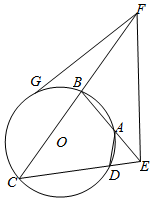 如图,四边形ABCD内接于⊙O,BA,CD的延长线相交于点E,EF∥DA,并与CB的延长线交于点F,FG切⊙O于G.
如图,四边形ABCD内接于⊙O,BA,CD的延长线相交于点E,EF∥DA,并与CB的延长线交于点F,FG切⊙O于G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
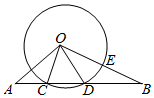 如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,OB与⊙O相交于点E,AC=4,CD=3,∠BOD=∠A,则BE=( )
如图,⊙O的半径为6,线段AB与⊙O相交于点C、D,OB与⊙O相交于点E,AC=4,CD=3,∠BOD=∠A,则BE=( )| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
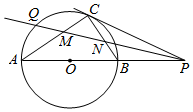 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,0) | C. | (1,-1) | D. | ($\frac{1}{2}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{7}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com