
分析 由题意,A、B1、P、B2构成矩形AB1PB2,以AB1,AB2所在直线为坐标轴建立直角坐标系,设出点O的坐标(x,y)与点P的坐标(a,b),求出x2+y2的取值范围,再求|$\overrightarrow{OA}$|的取值范围.
解答 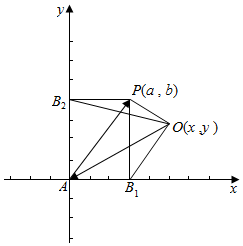 解:根据题意知,A、B1、P、B2构成一个矩形AB1PB2,
解:根据题意知,A、B1、P、B2构成一个矩形AB1PB2,
以AB1,AB2所在直线为坐标轴建立直角坐标系,如图所示;
设|AB1|=a,|AB2|=b,点O的坐标为(x,y),则点P的坐标为(a,b);
B1(a,0),B2(0,b),
由|$\overrightarrow{{OB}_{1}}$|=|$\overrightarrow{{OB}_{2}}$|=2,得$\left\{\begin{array}{l}{(x-a)^{2}+{y}^{2}=4}\\{{x}^{2}+(y-b)^{2}=4}\end{array}\right.$,则$\left\{\begin{array}{l}{(x-a)^{2}=4-{y}^{2}}\\{(y-b)^{2}=4-{x}^{2}}\end{array}\right.$;
∵|$\overrightarrow{OP}$|<1,∴(x-a)2+(y-b)2<1,
∴4-y2+4-x2<1,
∴x2+y2>7;①
又∵(x-a)2+y2=4,
∴y2=4-(x-a)2≤4,
∴y2≤4,
同理x2≤4,
∴x2+y2≤8;②
由①②知7<x2+y2≤8,
∵|$\overrightarrow{OA}$|=$\sqrt{{x}^{2}{+y}^{2}}$,
∴$\sqrt{7}$<|$\overrightarrow{OA}$|≤2$\sqrt{2}$.
故答案为:($\sqrt{7}$,2$\sqrt{2}$]
点评 本题考查了平面向量的应用问题,也考查了不等式的应用问题,根据条件建立坐标系,利用坐标法是解决本题的关键.考查学生的运算和推理能力,有一定的难度.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{4}{5}$ | C. | $-\frac{4}{5}$ | D. | $-\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
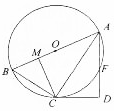 如图,AB是圆O的直径,C,F是圆O上的点,CA平分∠BAF,过C点作圆O的切线交AF的延长线于D点,CM⊥AB,垂足为M.
如图,AB是圆O的直径,C,F是圆O上的点,CA平分∠BAF,过C点作圆O的切线交AF的延长线于D点,CM⊥AB,垂足为M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
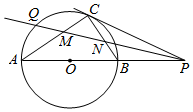 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示.
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示. | P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 晕机 | 不晕机 | 合计 | |
| 女 | 10 | 20 | 30 |
| 男 | 10 | 70 | 80 |
| 合计 | 20 | 90 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com