
| 喜爱网购 | 不喜爱网购 | 合计 | |
| 女 | 20 | 5 | 25 |
| 男 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
分析 (1)先求出抽取比例,由此能求出女性抽到的人数.
(2)记6人中,女性为A1,A2,A3,A4,男性为B1,B2,利用列举法能求出抽到的6人中选2人,恰好有一名男性的概率.
解答 解:(1)∵从喜欢网购的共30人中抽6人,抽取比例为$\frac{1}{5}$,
而女性共有20人,
∴女性抽到20×$\frac{1}{5}$=4人.
(2)记6人中,女性为A1,A2,A3,A4,男性为B1,B2,
所有的可能为(A1,A2),(A1,A3),(A1,A4),(A1,B1),(A1,B2),
(A2,A3),(A2,A4),(A2,B1),(A2,B2),(A3,A4),(A3,B1),
(A3,B2),(A4,B1),(A4,B2),(B1,B2)共有15种不同的抽法,
而恰好有一名男性有(A1,B1),(A1,B2),(A2,B1)(A2,B2),
(A3,B1),(A3,B2),(A4,B1),(A4,B2),共8种不同的方法,
∴恰有一名男性的概率为p=$\frac{8}{15}$.
点评 本题考查分层抽样的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
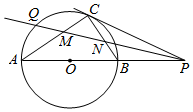 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示.
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示. | P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 晕机 | 不晕机 | 合计 | |
| 女 | 10 | 20 | 30 |
| 男 | 10 | 70 | 80 |
| 合计 | 20 | 90 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 线性回归直线一定过点(4.5,3.5) | |
| B. | 产品的生产能耗与产量呈正相关 | |
| C. | t的取值必定是3.15 | |
| D. | A产品每多生产1吨,则相应的生产能耗约增加0.7吨 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com