
分析 利用平方关系化简f(x)的解析式,设t=sinx则t∈[-1,1],代入原函数转化为关于t的二次函数,利用配方法化简,根据定义域对对称轴a进行分类讨论,分别由二次函数的单调性求出函数的最小值.
解答 解:f(x)=3-2asinx-cos2x=2-2asinx+sin2x,
设t=sinx则t∈[-1,1],则y=t2-2at+2=(t-a)2+2-a2,
①当a≤-1时,函数y=t2-2at+2在[-1,1]上递增,
∴当t=-1时,函数y取到最小值是:1+2a+2=2a+3,
②当-1<a<1时,当t=a时,y的最小值是-a2+2;
③当a≥1时,函数y=t2-2at+2在[-1,1]上递增减,
∴当t=1时,y的最小值是1-2a+2=-2a+3,
综上可得,${y_{min}}=\left\{{\begin{array}{l}{2a+3(a≤-1)}\\{-{a^2}+2(-1<a<1)}\\{-2a+3(a≥1)}\end{array}}\right.$.
点评 本题考查正弦函数的性质,平方关系,利用换元法将函数转化为二次函数的问题,考查分类讨论思想.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
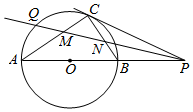 如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:
如图所示,点P是圆O直径AB延长线上的一点,PC切圆O于点C,直线PQ平分∠APC,分别交AC、BC于点M、N.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (0,0) | C. | (1,-1) | D. | ($\frac{1}{2}$,-$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示.
在一次飞机航程中调查男女乘客的晕机情况,男女乘客晕机与不晕机的人数如图所示. | P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 晕机 | 不晕机 | 合计 | |
| 女 | 10 | 20 | 30 |
| 男 | 10 | 70 | 80 |
| 合计 | 20 | 90 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 线性回归直线一定过点(4.5,3.5) | |
| B. | 产品的生产能耗与产量呈正相关 | |
| C. | t的取值必定是3.15 | |
| D. | A产品每多生产1吨,则相应的生产能耗约增加0.7吨 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $-\frac{1}{6}$ | C. | 6 | D. | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com