Question

【题目】设函数f（x）=aex+ +b（a＞0）．
（Ⅰ）求f（x）在[0，+∞）内的最小值；
（Ⅱ）设曲线y=f（x）在点（2，f（2））处的切线方程为y= ，求a，b的值．

Answer 1

【答案】解：（Ⅰ）设t=ex（t≥1），则
∴
①当a≥1时，y′≥0，∴ 在t≥1上是增函数，
∴当t=1（x=0）时，f（x）的最小值为
②当0＜a＜1时， ，当且仅当at=1（x=﹣lna）时，f（x）的最小值为b+2；
（Ⅱ）求导函数，可得）
∵曲线y=f（x）在点（2，f（2））处的切线方程为y= ，
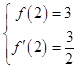∴ ，即 ，解得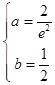
【解析】（Ⅰ）设t=ex（t≥1），则 ，求出导函数 ，再进行分类讨论：①当a≥1时，y′＞0， 在t≥1上是增函数；②当0＜a＜1时，利用基本不等式 ，当且仅当at=1（x=﹣lna）时，f（x）取得最小值；（Ⅱ）求导函数，利用曲线y=f（x）在点（2，f（2））处的切线方程为y= ，建立方程组，即可求得a，b的值．
【考点精析】认真审题，首先需要了解函数的最大(小)值与导数(求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值)．