
 )+2cos2(
)+2cos2( -x).
-x). )=
)= +1,c=
+1,c= ,cosB=
,cosB=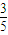 ,求b.
,求b. sin(2x+
sin(2x+ )+1.再由三角函数的周期公式和对称轴方程的公式,即可求出f(x)的最小正周期及对称轴方程;
)+1.再由三角函数的周期公式和对称轴方程的公式,即可求出f(x)的最小正周期及对称轴方程; )=
)= +1,得C=
+1,得C= .用同角三角函数的基本关系算出sinB=
.用同角三角函数的基本关系算出sinB= ,再利用正弦定理
,再利用正弦定理 的式子,代入数据即可求出边b的值.
的式子,代入数据即可求出边b的值. )+2cos2(
)+2cos2( -x)
-x) )+[1+cos(
)+[1+cos( -2x)]=
-2x)]= sin2x+
sin2x+ cos2x+1+sin2x
cos2x+1+sin2x sin2x+
sin2x+ cos2x+1=
cos2x+1= sin(2x+
sin(2x+ )+1
)+1 ,
, =
=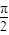 +kπ(k∈Z),得x=
+kπ(k∈Z),得x= (k∈Z)
(k∈Z) (k∈Z);
(k∈Z);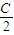 )=
)= sin(C+
sin(C+ )+1=
)+1=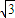 +1
+1 )=1,结合C∈(0,π)得C=
)=1,结合C∈(0,π)得C=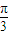
 ,可得sinB=
,可得sinB=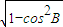 =
=
 ,得
,得 =
= =
= .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| ||
| 3 |
| ||
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com