
分析 (I)利用已知条件和变形等式an=4Sn-1+1推知数列{an}是等边数列,根据等比数列的通项公式进行解答;
(Ⅱ)利用(I)中的通项公式推知{|bn|}的通项公式.然后由分组求和法来求数列{|bn|}的前n项和Tn.
解答 解:(I)∵an+1=4Sn+1,①
∴当n≥2时,an=4Sn-1+1,②
由①-②,得
an+1-an=4(Sn-Sn-1)=4an(n≥2),
∴当n≥2时,an+1=5an(n≥2),
∴$\frac{{a}_{n+1}}{{a}_{n}}$=5.
∵S2=6,an+1=4Sn+1,n∈N*.
∴$\left\{\begin{array}{l}{{a}_{1}+{a}_{2}=6}\\{{a}_{2}=4{a}_{1}+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{a}_{1}=1}\\{{a}_{2}=5}\end{array}\right.$,
∴$\frac{{a}_{2}}{{a}_{1}}$=5,
∴数列{an}是首项a1=1,公比为5的等边数列,
∴an=5n-1;
(Ⅱ)由题意知|bn|=|5n-1-n-4|,n∈N*.
易知,当n≤2时,5n-1<n+4;当n≥3时,5n-1>n+4.
∴当n≤2时,|bn|=n+4-5n-1;
当n≥3时,|bn|=5n-1-(n+4),
∴T1=b1=4,T2=b1+b2=5.
当n≥3时,Tn=T2+b2+b3+…+bn
=5+[52-(3+4)+[52-(4+4)]+…+[5n-1-(n+4)]
=5+(52+53+…+5n-1)-[(3+4)+(4+4)+…+(n+4)]
=5+$\frac{{5}^{2}(1-{5}^{n-2})}{1-5}$-$\frac{(n-2)(7+n+4)}{2}$
=$\frac{{5}^{n}-2{n}^{2}-18n+39}{4}$.
又∵T1=4不满足上式,T2=5满足上式,
∴Tn=$\left\{\begin{array}{l}{4,(n=1)}\\{\frac{{5}^{n}-2{n}^{2}-18n+39}{4},n≥2,n∈{N}^{+}}\end{array}\right.$.
点评 本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意等比数列的定义的灵活运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
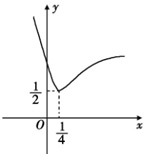 如图所示的函数F(x)的图象,由指数函数f(x)=ax与幂函数g(x)=xb“拼接”而成.
如图所示的函数F(x)的图象,由指数函数f(x)=ax与幂函数g(x)=xb“拼接”而成.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈(0,+∞),lnx≠x-2 | B. | ?x∉(0,+∞),lnx=x-2 | ||
| C. | ?x0∈(0,+∞),使lnx0≠x0-2 | D. | ?x0∉(0,+∞),lnx0=x0-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com