
如图所示,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.

(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求二面角F-BC-A的余弦值.
(1)见解析(2)见解析(3)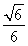
【解析】(1)证明:∵平面ABC∥平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,∴AB∥DE.
又∵AB=DE,∴四边形ADEB为平行四边形,∴BE∥AD.
∵AD⊥平面DEFG,∴BE⊥平面DEFG.
(2)证明:设DG的中点为M,联结AM,MF,则DM= DG=2,
DG=2,

∵EF=2,EF∥DG,∴四边形DEFM是平行四边形,
∴MF=DE且MF∥DE,由(1)知,四边形ADEB为平行四边形,∴AB=DE且AB∥DE,∴AB=MF且AB∥MF,
∴四边形ABFM是平行四边形,
即BF∥AM,又BF?平面ACGD,AM?平面ACGD,故BF∥平面ACGD.

(3)由已知,AD,DE,DG两两垂直,建立如图所示的空间直角坐标系,则A(0,0,4),B(2,0,4),C(0,1,4),F(2,2,0),
故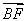 =(0,2,-4),
=(0,2,-4),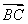 =(-2,1,0).
=(-2,1,0).
设平面FBC的法向量为n1=(x,y,z),则
令z=1,则n1=(1,2,1),
而平面ABC的法向量可为n2=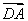 =(0,0,4),
=(0,0,4),
则cos〈n1,n2〉=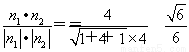 ,
,
由图形可知,二面角F-BC-A的余弦值为-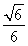


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:填空题
若函数f(x)=x2-|x+a|为偶函数,则实数a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:解答题
已知圆C1:x2+y2-2y=0,圆C2:x2+(y+1)2=4的圆心分别为C1,C2,P为一个动点,且直线PC1,PC2的斜率之积为- .
.
(1)求动点P的轨迹M的方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得|C1C|=|C1D|?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:填空题
若不等式x2+2xy≤a(x2+y2)对于一切正数x,y恒成立,则实数a的最小值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:选择题
由曲线xy=1,直线y=x,y=3所围成的平面图形的面积为( )
A.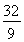 B.2-ln 3 C.4+ln 3 D.4-ln 3
B.2-ln 3 C.4+ln 3 D.4-ln 3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题五练习卷(解析版) 题型:选择题
网格纸中的小正方形边长为1,一个正三棱锥的侧视图如图所示,则这个正三棱锥的体积为( )

A. B.3
B.3 C.
C.  D.
D. 

查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题三练习卷(解析版) 题型:解答题
函数f(x)=sin(ωx+φ)ω>0,|φ|< 的部分图像如图Z3-4所示,将y=f(x)的图像向右平移
的部分图像如图Z3-4所示,将y=f(x)的图像向右平移 个单位长度后得到函数y=g(x)的图像.
个单位长度后得到函数y=g(x)的图像.

(1)求函数y=g(x)的解析式;
(2)在△ABC中,它的三个内角满足2sin2 =gC+
=gC+ +1,且其外接圆半径R=2,求△ABC的面积的最大值.
+1,且其外接圆半径R=2,求△ABC的面积的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题一练习卷(解析版) 题型:选择题
某程序框图如图所示,该程序运行后,输出x的值为31,则a等于( )
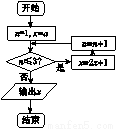
A.0 B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com