
已知圆C1:x2+y2-2y=0,圆C2:x2+(y+1)2=4的圆心分别为C1,C2,P为一个动点,且直线PC1,PC2的斜率之积为- .
.
(1)求动点P的轨迹M的方程;
(2)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C,D,使得|C1C|=|C1D|?若存在,求直线l的方程;若不存在,请说明理由.
(1) +y2=1(x≠0)(2)不存在
+y2=1(x≠0)(2)不存在
【解析】(1)两圆的圆心坐标分别为C1(0,1),和C2(0,-1),
设动点P的坐标为(x,y),则直线PC1,PC2的斜率分别为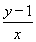 (x≠0)和
(x≠0)和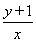 (x≠0).
(x≠0).
由已知条件得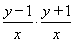 =-
=-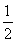 (x≠0),即
(x≠0),即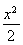 +y2=1(x≠0).
+y2=1(x≠0).
所以动点P的轨迹M的方程为 +y2=1(x≠0).
+y2=1(x≠0).
(2)假设存在满足条件的直线l,易知点A(2,0)在椭圆M的外部,当直线l的斜率不存在时,直线l与椭圆M无交点,此时不符合题意,所以直线l斜率存在,设为k,则直线l的方程为y=k(x-2).
联立方程组 得(2k2+1)x2-8k2x+8k2-2=0,①
得(2k2+1)x2-8k2x+8k2-2=0,①
依题意Δ=-8(2k2-1)>0,解得- <k<
<k<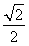 .
.
当-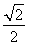 <k<
<k<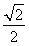 时,设交点分别为C(x1,y1),D(x2,y2),CD的中点为N(x0,y0),
时,设交点分别为C(x1,y1),D(x2,y2),CD的中点为N(x0,y0),
则x1+x2=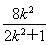 ,则x0=
,则x0=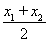 =
=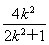 ,
,
所以y0=k(x0-2)=k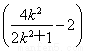 =
=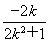 .
.
要使|C1C|=|C1D|,必须C1N⊥l,即k·kC1N=-1,
所以k· =-1,即k2-k+
=-1,即k2-k+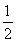 =0,
=0,
因为Δ1=1-4×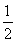 =-1<0,∴k2-k+
=-1<0,∴k2-k+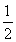 =0无解,
=0无解,
所以不存在直线,使得|C1C|=|C1D|,
综上所述,不存在直线l,使得|C1C|=|C1D|.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
已知曲线f(x)=ln x在点(x0,f(x0))处的切线经过点(0,-1),则x0的值为( )
A. B.1
B.1
C.e D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:填空题
已知全集U=R,Z是整数集,集合A={x|x2-x-6≥0,x∈R},则Z∩∁UA中元素的个数为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:填空题
如图所示的图形由小正方形组成,请观察图①至图④的规律,并依此规律,得第n个图形中小正方形的个数是________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:选择题
已知在等比数列{an}中,有a3a11=4a7,数列{bn}是等差数列,且a7=b7,则b5+b9=( )
A.2 B.4 C.8 D.16
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:填空题
已知抛物线方程为x2=4y,过点M(0,m)的直线交抛物线于A(x1,y1),B(x2,y2)两点,且x1x2=-4,则m的值为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题六练习卷(解析版) 题型:选择题
过点A(2,3)且垂直于直线2x+y-5=0的直线方程为( )
A.x-2y+4=0 B.2x+y-7=0
C.x-2y+3=0 D.x-2y+5=0
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题五练习卷(解析版) 题型:解答题
如图所示,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.

(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求二面角F-BC-A的余弦值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题三练习卷(解析版) 题型:选择题
△ABC的三个内角A,B,C的对边分别a,b,c,且acos C,bcos B,ccos A成等差数列,则角B等于( )
A.30° B.60° C.90° D.120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com