
【题目】在湖北新冠疫情严重期间,我市响应国家号召,召集医务志愿者组成医疗队驰援湖北.某医院有2名女医生,3名男医生,3名女护士,1名男护士报名参加,医院计划从医生和护士中各选2名参加医疗队.
(1)求选出的4名志愿全是女性的选派方法数;
(2)记![]() 为选出的4名选手中男性的人数,求
为选出的4名选手中男性的人数,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知首项相等的两个数列![]() 满足
满足![]() .
.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若![]() ,求
,求![]() 的前n项和
的前n项和![]() ;
;
(3)在(2)的条件下,数列![]() 是否存在不同的三项构成等比数列?如果存在,请你求出所有符合题意的项;若不存在,请说明理由.
是否存在不同的三项构成等比数列?如果存在,请你求出所有符合题意的项;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
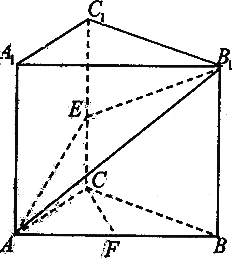
【题目】如图,直三棱柱![]() 中,
中,![]() 且
且![]() ,
,![]() 是棱
是棱![]() 上的动点,
上的动点,![]() 是
是![]() 的中点.
的中点.
(1)当![]() 是
是![]() 中点时,求证:
中点时,求证:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ,若存在,求
,若存在,求![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的左、右焦点分别是
的左、右焦点分别是![]() 、
、![]() ,左、右两顶点分别是
,左、右两顶点分别是![]() 、
、![]() ,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点
,弦AB和CD所在直线分别平行于x轴与y轴,线段BA的延长线与线段CD相交于点![]() 如图).
如图).
⑴若![]() 是
是![]() 的一条渐近线的一个方向向量,试求
的一条渐近线的一个方向向量,试求![]() 的两渐近线的夹角
的两渐近线的夹角![]() ;
;
⑵若![]() ,
,![]() ,
,![]() ,
,![]() ,试求双曲线
,试求双曲线![]() 的方程;
的方程;
⑶在⑴的条件下,且![]() ,点C与双曲线的顶点不重合,直线
,点C与双曲线的顶点不重合,直线![]() 和直线
和直线![]() 与直线l:
与直线l:![]() 分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.
分别相交于点M和N,试问:以线段MN为直径的圆是否恒经过定点?若是,请求出定点的坐标;若不是,试说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地环保部门跟踪调查一种有害昆虫的数量.根据调查数据,该昆虫的数量![]() (万只)与时间
(万只)与时间![]() (年)(其中
(年)(其中![]() )的关系为
)的关系为![]() .为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值
.为有效控制有害昆虫数量、保护生态环境,环保部门通过实时监控比值![]() (其中
(其中![]() 为常数,且
为常数,且![]() )来进行生态环境分析.
)来进行生态环境分析.
(1)当![]() 时,求比值
时,求比值![]() 取最小值时
取最小值时![]() 的值;
的值;
(2)经过调查,环保部门发现:当比值![]() 不超过
不超过![]() 时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数
时不需要进行环境防护.为确保恰好3年不需要进行保护,求实数![]() 的取值范围.(
的取值范围.(![]() 为自然对数的底,
为自然对数的底, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,![]() 为
为![]() 中点,
中点,

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是正三角形,且
是正三角形,且![]() .
.
(Ⅰ)当点![]() 在线段
在线段![]() 上什么位置时,有
上什么位置时,有![]() 平面
平面![]() ?
?
(Ⅱ)在(Ⅰ)的条件下,点![]() 在线段
在线段![]() 上什么位置时,有平面
上什么位置时,有平面![]() 平面
平面![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沙漏是我国古代的一种计时工具,是用两个完全相同的圆锥顶对顶叠放在一起组成的(如图).在一个圆锥中装满沙子,放在上方,沙子就从顶点处漏到另一个圆锥中,假定沙子漏下来的速度是恒定的.已知一个沙漏中沙子全部从一个圆锥中漏到另一个圆锥中需用时10分钟.那么经过5分钟后,沙漏上方圆锥中的沙子的高度与下方圆锥中的沙子的高度之比是(假定沙堆的底面是水平的)( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com