
分析 (1)直接利用复数代数形式的乘除运算化简求值;
(2)求出$\overline{Z}$,由其实部大于0且虚部大于0联立不等式组求解.
解答 解:(1)$\frac{{(1-i)+(2+\sqrt{5}i)}}{i}$=$\frac{3+(\sqrt{5}-1)i}{i}=\frac{[3+(\sqrt{5}-1)i](-i)}{-{i}^{2}}$=$\sqrt{5}-1-3i$;
(2)复数Z=(2m2+m-1)+(4m2-8m+3)i,的共轭复数$\overline Z$(2m2+m-1)-(4m2-8m+3)i,
由复数$\overline Z$对应的点在第一象限,得:
$\left\{\begin{array}{l}{2{m}^{2}+m-1>0}\\{4{m}^{2}-8m+3<0}\end{array}\right.$,解得$\frac{1}{2}$<m<$\frac{3}{2}$.
∴实数m的取值集合为{m|$\frac{1}{2}<m<\frac{3}{2}$}.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,6) | B. | (4,6) | C. | {4,5,6} | D. | {5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
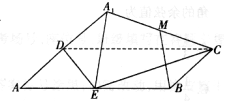 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com