
| A. | 16 | B. | 20 | C. | 18 | D. | 24 |
分析 解法一:消元法,消去其中一个参数后,利用基本不等式求解最小值.
解法二,“乘1法”与基本不等式的性质求解.
解答 解:解法一:消元法
∵2x+8y-xy=0
∴y=$\frac{2x}{x-8}$
又∵x>0,y>0,
∴x-8>0
那么:x+y=x+$\frac{2x}{x-8}$=$\frac{{x}^{2}-6x}{x-8}$=$\frac{(x-8)^{2}+10(x-8)+16}{x-8}$=$(x-8)+\frac{16}{x-8}+10≥2\sqrt{16}+10=18$
当且仅当x=12,y=6时取等号.
解法二,直接利用基本不等式
∵x>0,y>0,2x+8y=xy
那么:$\frac{2}{y}+\frac{8}{x}=1$
x+y=(x+y)($\frac{2}{y}+\frac{8}{x}$)=10+$\frac{2x}{y}+\frac{8y}{x}$$≥2\sqrt{16}$+10=18
当且仅当x=12,y=6时取等号.
故选:C
点评 本题考查了基本不等式的灵活运用能力.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin|x| | B. | y=cos|x| | C. | y=|tanx| | D. | y=-ln|sinx| |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
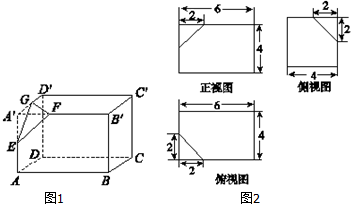
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com