Question

6．如图1是一个长方体截去一个角所得多面体的直观图和三视图．（单位：cm）

（1）求该多面体的体积；
（2）在所给直观图中连结BC′，证明：BC′∥平面EFG．

Answer 1

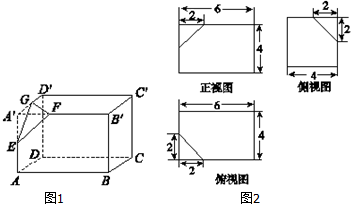
分析 （1）所求多面体体积V=V_长方体-V_正三棱锥，由此能求出结果．
（2）连结AD'，则AD'∥BC'，AD'∥EG，从而EG∥BC'．由此能证明BC'∥面EFG．

解答 （1）解：由题意可得，所求多面体体积：
V=V_长方体-V_正三棱锥=$4×4×6-\frac{1}{3}（\frac{1}{2}×2×2）×2$=$\frac{284}{3}c{m}^{3}$；
（2）证明：在长方体ABCD-A'B'C'D'中，
连结AD'，则AD'∥BC'．
因为E，G分别为AA'，A'D'中点，
所以AD'∥EG，
从而EG∥BC'．又BC'?平面EFG，
所以BC'∥面EFG．

点评 本题主要考查由三视图求面积、体积，求解的关键是由视图得出几何体的长、宽、高等性质，熟练掌握各种类型的几何体求体积的公式；熟练掌握证明线面问题的有关定理．