
 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,CA=CB,D,E,F分别为AB,A1D,A1C的中点,点G在AA1上,且A1D⊥EG.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1⊥底面ABC,CA=CB,D,E,F分别为AB,A1D,A1C的中点,点G在AA1上,且A1D⊥EG.分析 (1)利用三角形的中位线的性质,证明EF∥CD,利用线面平行的判定定理证明:CD∥平面EFG;
(2)利用等腰三角形三线合一证明CD⊥AB,利用平面与平面垂直的性质证明CD⊥A1D,利用线面垂直的判定定理证明:A1D⊥平面EFG.
解答 证明:(1)∵E,F分别为A1D,A1C的中点,
∴EF∥CD,
∵CD?平面EFG,EF?平面EFG,
∴CD∥平面EFG;
(2)∵CA=CB,D为AB的中点,
∴CD⊥AB,
∵侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,
∴CD⊥侧面ABB1A1,
∴CD⊥A1D,
∵EF∥CD,
∴A1D⊥EF,
∵A1D⊥EG,EF∩EG=E,
∴A1D⊥平面EFG.
点评 本题考查线面平行,线面垂直,解题的关键是正确运用线面平行、线面垂直的判定,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 算法的三种基本结构是顺序结构、条件结构,循环结构 | |
| B. | 用样本频率分布估计总体频率分布的过程中,总体容量越大,估计越精确 | |
| C. | 一组数据的方差为3,将这组数据中的每一个数据都扩大到原来的3倍,所得的新数据组的方差还是3 | |
| D. | 有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为5,15,20,35,40 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\stackrel{∧}{y}$=2x-2.1 | B. | $\stackrel{∧}{y}$=-2x+9.5 | C. | $\stackrel{∧}{y}$=0.3x+2.6 | D. | $\stackrel{∧}{y}$=-0.3x+4.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.
如图,已知抛物线C1:y2=4x的焦点为F,椭圆C2的中心在原点,F为其右焦点,点M为曲线C1和C2在第一象限的交点,且|$\overrightarrow{MF}$|=$\frac{5}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
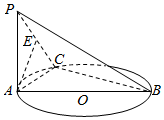 如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,$AB=\sqrt{3}$,PA=AC=1.
如图,AB是圆O的直径,C是圆O上不同于A,B的一点,PA⊥平面ABC,E是PC的中点,$AB=\sqrt{3}$,PA=AC=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com