
分析 (1)由焦距的概念和a,b,c的关系,及正三角形的概念,即可得到a,b方程,解方程可得椭圆的方程;
(2)设T点的坐标为(-3,m),运用直线的斜率公式,由垂直的条件,可得直线PQ的方程,代入椭圆方程,运用韦达定理和中点坐标公式,设PQ的中点为M,结合斜率公式,可得直线OT和OM的斜率相等,即可得证.
解答 解:(1)由已知可得,c=$\sqrt{{a}^{2}-{b}^{2}}$=2,2b=$\sqrt{{a}^{2}+{b}^{2}}$,
解得a2=6,b2=2,
所以椭圆C的标准方程是$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1;
(2)证明:由(1)可得,F的坐标是(-2,0),
设T点的坐标为(-3,m),
则直线TF的斜率kTF=$\frac{m-0}{-3-(-2)}$=-m.
当m≠0时,直线PQ的斜率kPQ=$\frac{1}{m}$.直线PQ的方程是x=my-2.
当m=0时,直线PQ的方程是x=-2,也符合x=my-2的形式.
设P(x1,y1),Q(x2,y2),
将直线PQ的方程与椭圆C的方程联立,
消去x,得(m2+3)y2-4my-2=0,
其判别式△=16m2+8(m2+3)>0.
所以y1+y2=$\frac{4m}{3+{m}^{2}}$,y1y2=$\frac{-2}{3+{m}^{2}}$,
x1+x2=m(y1+y2)-4=$\frac{-12}{3+{m}^{2}}$.
设M为PQ的中点,则M点的坐标为($\frac{-6}{3+{m}^{2}}$,$\frac{2m}{3+{m}^{2}}$),
所以直线OM的斜率kOM=-$\frac{m}{3}$,又直线OT的斜率kOT=-$\frac{m}{3}$,
所以点M在直线OT上,因此OT平分线段PQ.
点评 本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,运用韦达定理,斜率公式和中点坐标公式,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最大值是f(1),最小值是f(3) | B. | 最大值是f(3),最小值是f(1) | ||
| C. | 最大值是f(1),最小值是f(2) | D. | 最大值是f(2),最小值是f(3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
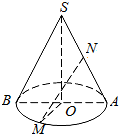 已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.
已知圆锥的底面半径r=2,半径OM与母线SA垂直,N是SA中点,NM与高SO所成的角为α,tanα=2.则圆锥的体积为$\frac{4\sqrt{5}}{3}π$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 08 | B. | 07 | C. | 02 | D. | 01 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
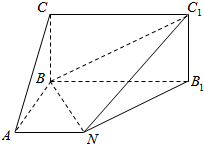 如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.
如图,矩形BB1C1C所在平面与底面ANB1B垂直,在直角梯形ANB1B中,AB⊥AN,CB=BA=AN=4,BB1=8,AN∥BB1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com